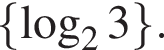На діаграмі показано кількість покупців під час проведення акції у магазині. В який день кількість покупців товару за акцією склала менше 30% від кількості всіх покупців у цей день?
На одній чаші врівноважених ваг лежать 3 яблука та 1 груша, на іншій — 2 яблука, 2 груші та гирка вагою 20 г. Яка вага одного яблука (у грамах), якщо всі фрукти разом важать 780 г? Вважайте, що всі яблука однакові за вагою та всі груші однакові за вагою.
Дано дві правильні чотирикутні піраміди. Об єм першої піраміди дорівнює 16. У другої піраміди висота в 2 рази більша, а сторона основи в 1,5 рази більша, ніж у першої. Знайдіть об’єм другої піраміди.
Укажіть корінь рівняння 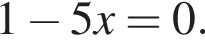
На колі з центром О вибрано точки А та В (див. рисунок). Визначте градусну міру кута АОВ, якщо довжина дуги
![]() становить
становить ![]() довжини цього кола.
довжини цього кола.
На рисунку зображено графік функції
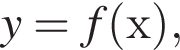 визначеної на проміжку [−4; 6]. Укажіть найбільшв значення функції f на цьому проміжку.
визначеної на проміжку [−4; 6]. Укажіть найбільшв значення функції f на цьому проміжку.
Спростіть вираз 
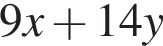
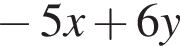


Потужність постійного струму (у Вт) обчислюється за формулою P = I 2 R , де I - сила струму (в амперах), R - опір (в омах). Використовуючи цю формулу, знайдіть опір R (в омах), якщо потужність становить 150 Вт, а сила струму дорівнює 5 амперам.
Спростіть вираз 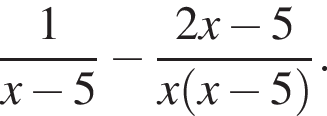
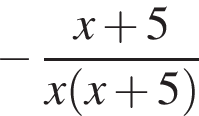
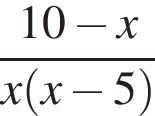
Які з наведених тверджень є правильними?
I. Якщо дуга кола становить 80°, то вписаний кут, що спирається на цю дугу кола, дорівнює 40°.
II. Центром кола, вписаного в трикутник, є точка перетину серединних перпендикулярів до його сторін.
III. Серединні перпендикуляри до сторін трикутника перетинаються в центрі описаного кола.
Розв’яжіть систему рівнянь
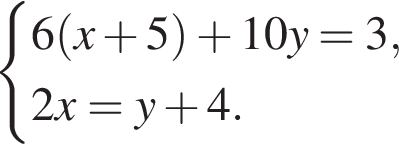
Для одержаного розв’язку 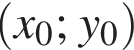 укажіть суму
укажіть суму 
Використовуючи формулу Ньютона-Лейбніца, обчисліть 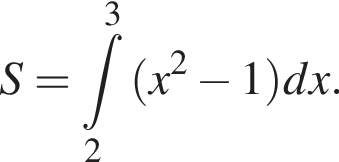
Розв’яжіть систему нерівностей: 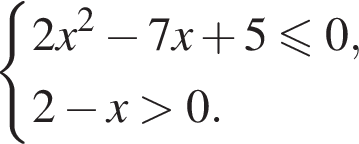
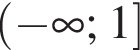
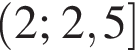
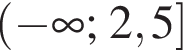
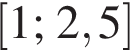
Знайдіть значення виразу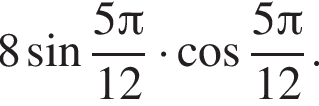
Площа бічної поверхні циліндра дорівнює 24π, а довжина кола його основи — 4π. Визначте висоту цього циліндра.
У коробку у формі прямокутного паралелепіпеда щільно укладено у 2 ряди10 шматочків крейди (див. лівий рис.). Кожний шматочок має форму циліндра висотою 10 см і діаметром основи 15 мм (див. правий рисунок). Визначте площу плівки, якою в один шар щільно з усіх боків без накладань обгорнуто цю коробку. Місцями з’єднання плівки та товщиною стінок коробки знехтуйте.
Увідповідніть функцію (1–3) та її властивість (А–Д).
1 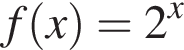
2 
3 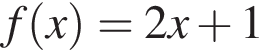
А функція непарна
Б областю значень функції є множина 
В областю визначення функції є проміжок 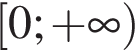
Г функція спадає на проміжку 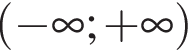
Д графік функції має лише дві точки перетину з осями координат
Установіть відповідність між виразом (1–3) та проміжком (А–Д), якому належить його значення.
1 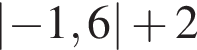
2 ![]()
3 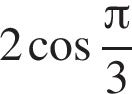
А 
Б ![]()
В ![]()
Г ![]()
Д 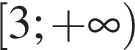
Основи ВС й AD рівнобічної трапеції ABCD дорівнюють 7 см і 25 см відповідно. Діагональ трапеції BD перпендикулярна до бічної сторони АВ. До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
1. Середня лінія трапеції дорівнює
2. Проекція сторони AB на пряму AD дорівнює
3. Висота трапеції дорівнює
4. Сторона AB трапеції дорівнює
А 9 см
Б 12 см
В 15 см
Г 16 см
Д 18 см
Установіть відповідність між вимірами циліндра (1−3) та правильним щодо нього твердженням (А−Д).
1. радіус основи дорівнює 6, висота — 4
2. радіус основи дорівнює 2, висота — 6
3. радіус основи дорівнює 4, висота — 6
А циліндр утворено обертанням прямокутника зі сторонами 4 та 6 навколо більшої сторони
Б площа основи циліндра дорівнює 12π
В твірна циліндра дорівнює 4
Г площа бічної поверхні циліндра дорівнює 24π
Д об'єм цилiндра дорівнює 48π
У дитячому шаховому клубі функціонують лише молодша й старша групи. Старшу групу відвідують 27 дітей. Відвідувачі молодшої групи становлять 46% від загальної кількості відвідувачів обох груп шахового клубу.
1. Визначте кiлькiсть дiтей у молодшiй групi.
2. Скільки дітей потрібно додатково набрати в молодшу групу за умови незмінності кількості дітей старшої групи, щоб відношення кількості відвідувачів молодшої групи до кількості відвідувачів старшої групи становило 4 : З?
Діагональ BD прямокутної трапеції ABCD є бісектрисою кута ADC й утворює з основою AD кут 30° (див. рисунок). Визначте довжину середньої лінії трапеції ABDC (у см), якщо

В прямоугольной системе координат в пространстве заданы точки А (1; 3; −8) и B (6; −5; –10).
1. Найдите координаты вектора ![]() В ответе напишите их сумму.
В ответе напишите их сумму.
2. Найдите модуль вектора ![]() В ответ запишите квадрат найденного модуля.
В ответ запишите квадрат найденного модуля.
Виписано кілька послідовних членів геометричної прогресії: …; 150; x; 6; 1,2; …
1. Найдите знаменатель данной геометрической прогрессии.
2. Знайдіть член прогресії, позначений літерою x.
На виборах президента школи балотуються три кандидати: Наталя, Микола й Антон. За результатами опитування ймовірність того, що переможе Антон, дорівнює ймовірності того, що переможе Микола, й вдвічі менша за ймовірність того, що переможе Наталя. Якою за результатами опитування є ймовірність того, що президентом школи оберуть Миколу?
Фабрика виготовляє комплекти пластикових меблів, кожен з яких складається зі стола, дивана та двох крісел. На виготовлення дивана витрачається на 1 кг пластику більше, ніж на виготовлення стола, та на 3 кг більше, ніж на виготовлення одного крісла. Відомо, що на виготовлення 10 крісел витрачається пластику стільки ж, як і на виготовлення 2 столів та 4 диванів разом. Скільки кілограмів пластику витрачається на виготовлення одного комплекту пластикових меблів?
Обчисліть 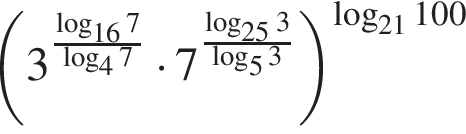 .
.
Розв'яжіть рівняння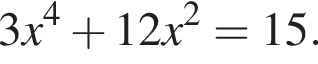 У відповідь запишіть добуток усіх його дійсних коренів.
У відповідь запишіть добуток усіх його дійсних коренів.
На курсах з вивчення іноземних мов як бонус запропоновано два безкоштовні заняття, одне з яких проводитимуть дистанційно, а друге — в аудиторії. Тему кожного з цих двох занять слухач може вибрати самостійно з 10 запропонованих. Скільки всього існує способів вибору форм проведення цих двох занять та різних тем до них?
| x | y |
|---|---|
| −2 | |
| −1 | |
Задано функцію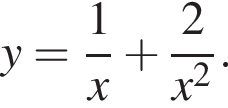
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення у (див. таблицю).
2. Знайдіть похідну f' функції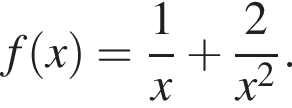 Визначте нульові функції f' .
Визначте нульові функції f' .
3. Напишіть рівняння графіку функції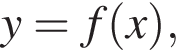 паралельної осі абсцис.
паралельної осі абсцис.
4. Визначте проміжки зростання та спадання, точки екстремуму функції f .
5. Знайдіть найбільше та найменше значення функції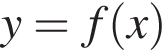 на відрізку
на відрізку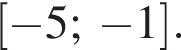
6. Побудуйте графік функції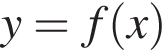 на відрізку
на відрізку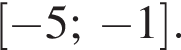
Бічні ребра правильної трикутної піраміди дорівнюють 5. Плоский кут при вершині дорівнює γ.
1. Зобразіть на малюнку цю піраміду та кут γ.
2. Знайдіть площу основи.
3. Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3492) бічні ребра правильної трикутної піраміди дорівнюють 6. Плоский кут при вершині дорівнює γ.
а) Зобразіть на малюнку цю піраміду і побудуйте лінійний кут двогранного кута при основі піраміди.
б) Знайдіть цей кут.
Доведіть тотожність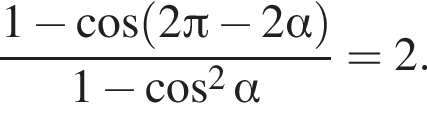
Задано систему рівнянь
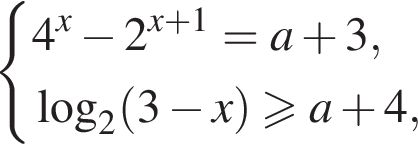
1. Розв'яжіть рівняння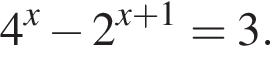
2. Визначте всі значення параметра, а при кожному з яких система має рівно два рішення.

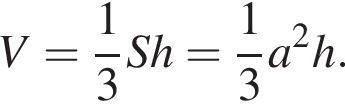 Следовательно, отношение объёмов пирамид:
Следовательно, отношение объёмов пирамид: 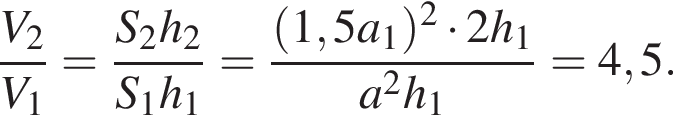
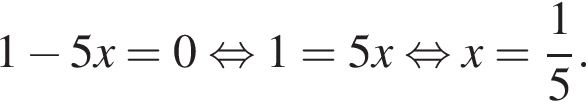
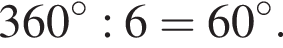
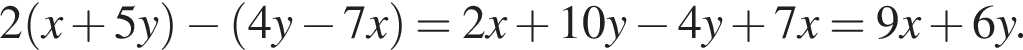
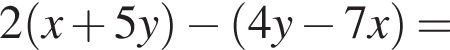
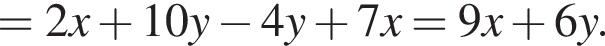
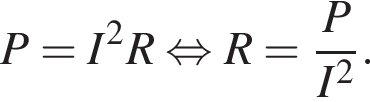
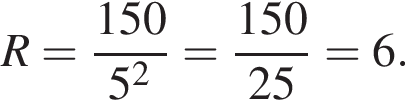
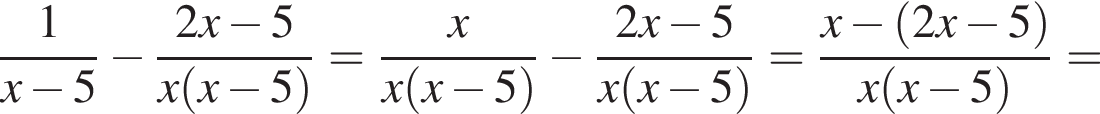
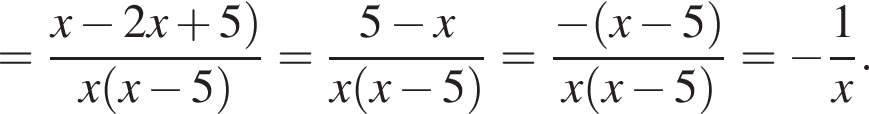
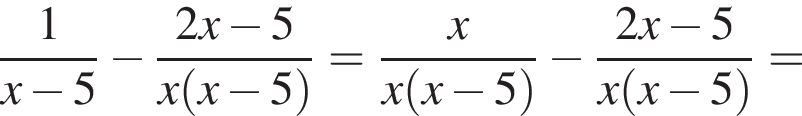
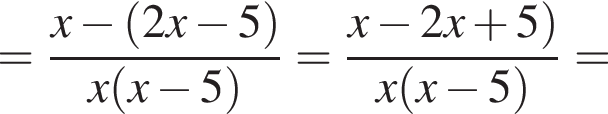
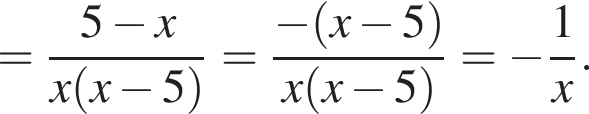
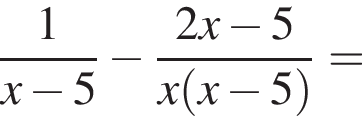
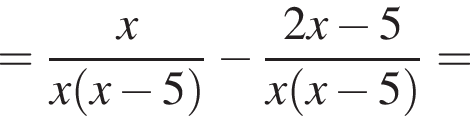
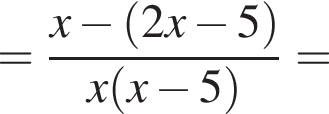
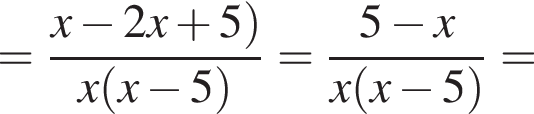
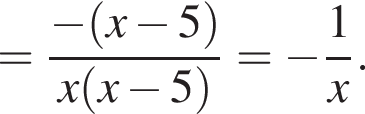
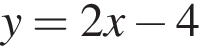 и подставим в первое. Получим
и подставим в первое. Получим 
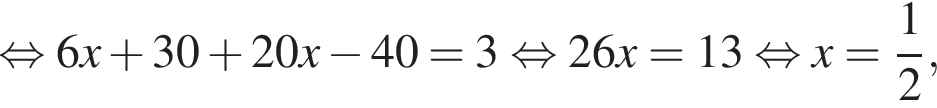

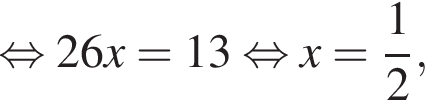
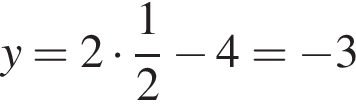
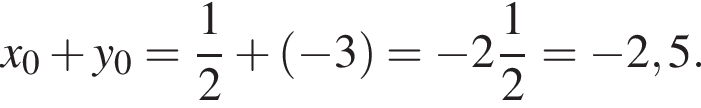
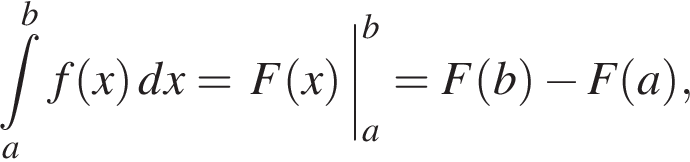
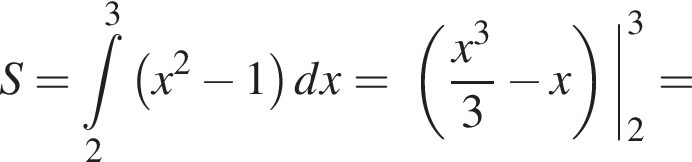
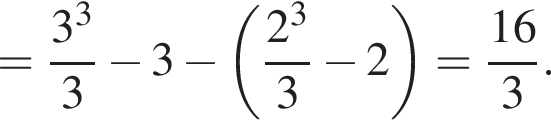
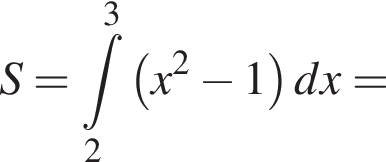
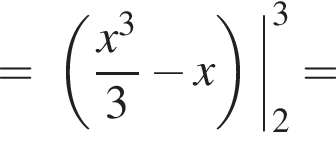
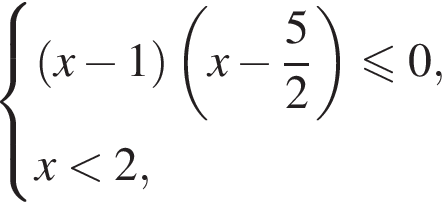
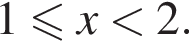
 :
: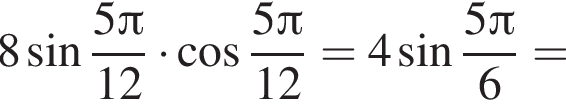
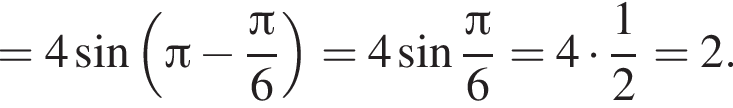
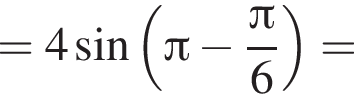
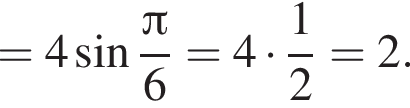
 откуда
откуда  откуда
откуда  и
и 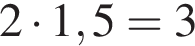 см
см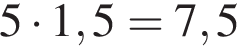 см
см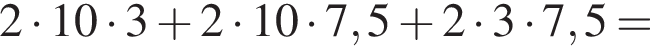
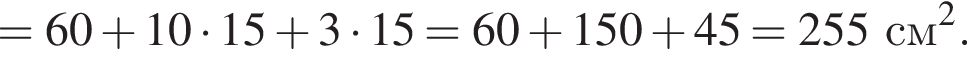
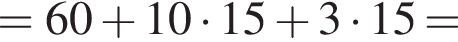
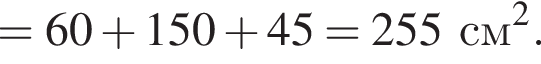
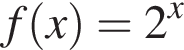 не принимает отрицательных значений ни при каких значениях x, а значит, областью ее определения является промежуток
не принимает отрицательных значений ни при каких значениях x, а значит, областью ее определения является промежуток  Ответ — Б.
Ответ — Б.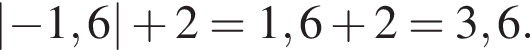 Данное значение соответствует промежутку
Данное значение соответствует промежутку  Ответ — Д.
Ответ — Д.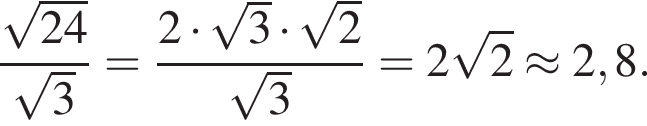 Данное значение соответствует промежутку
Данное значение соответствует промежутку 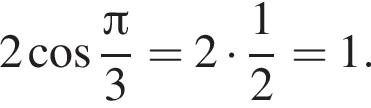 Данное значение соответствует промежутку
Данное значение соответствует промежутку 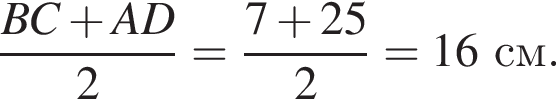
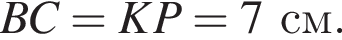 Найдем длину AK:
Найдем длину AK: 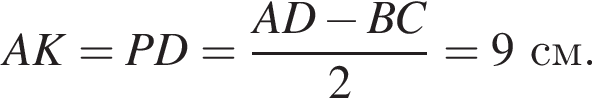
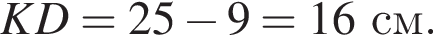

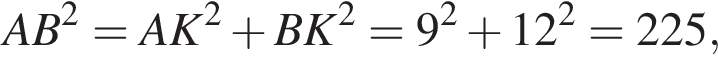
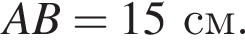
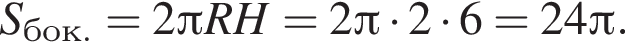 Итак, 2 — Г.
Итак, 2 — Г. 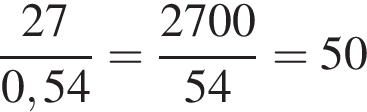



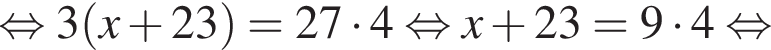
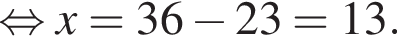
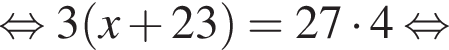
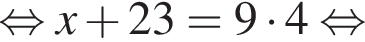
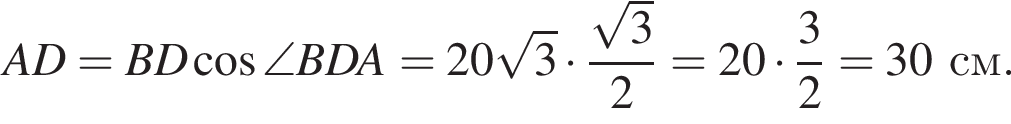
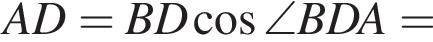
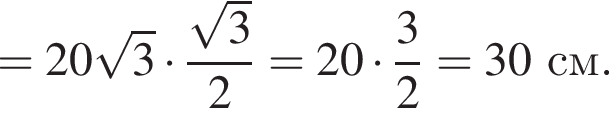
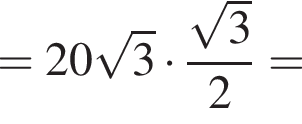
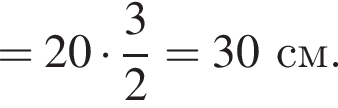
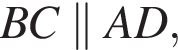 углы
углы 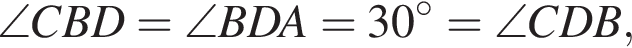
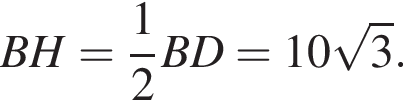 В прямоугольном треугольнике BCH находим
В прямоугольном треугольнике BCH находим 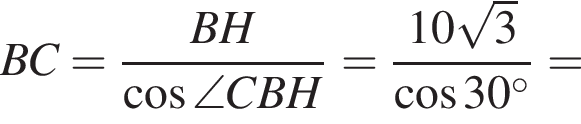
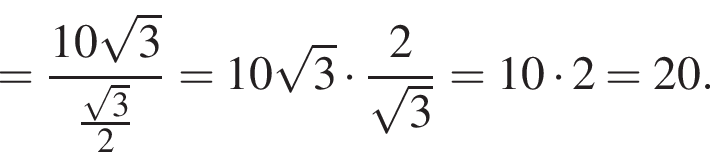
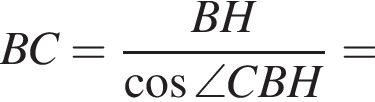
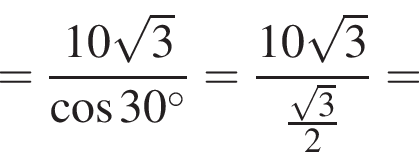
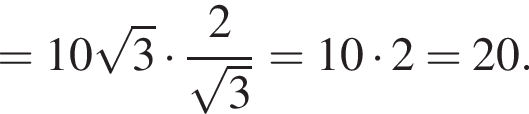
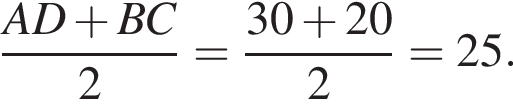

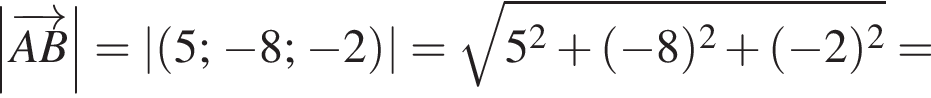
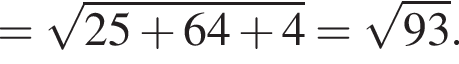
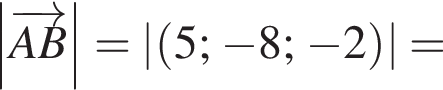
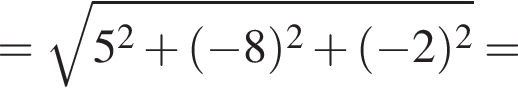
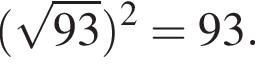
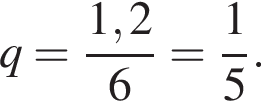 Поэтому,
Поэтому, 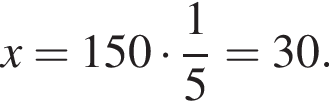
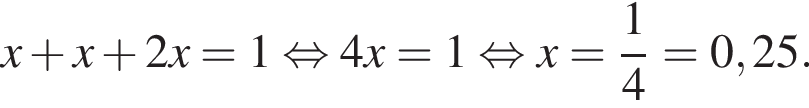
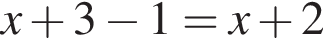 килограммов пластика. По условию
килограммов пластика. По условию 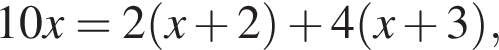 откуда
откуда 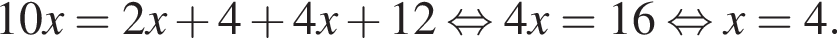
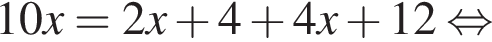
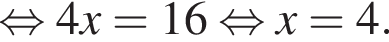
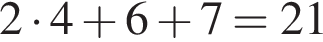 кг.
кг.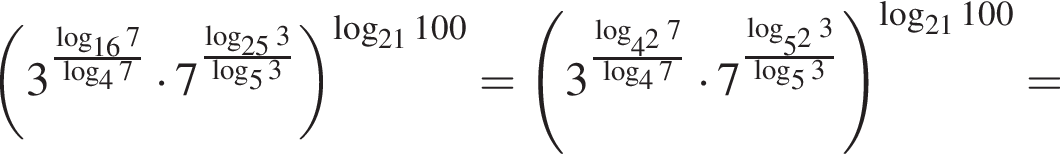
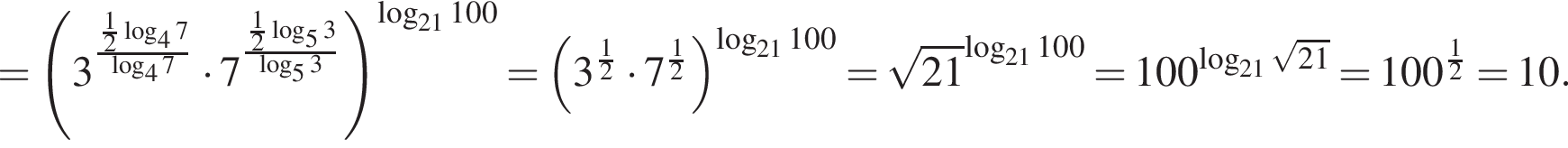
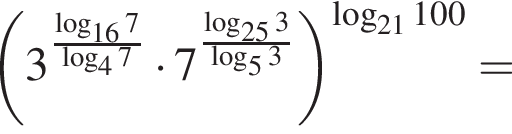
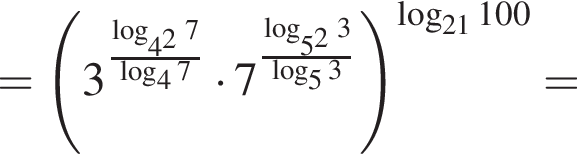
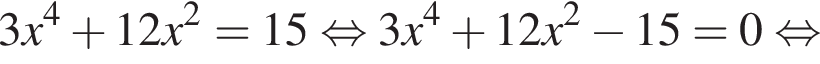
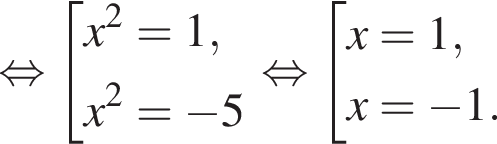
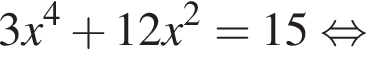
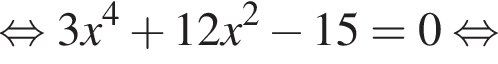
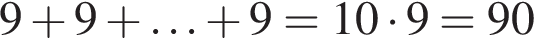
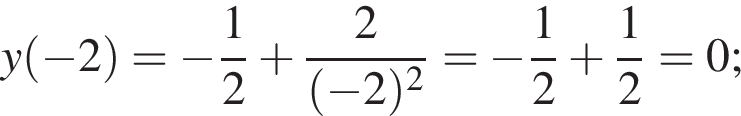
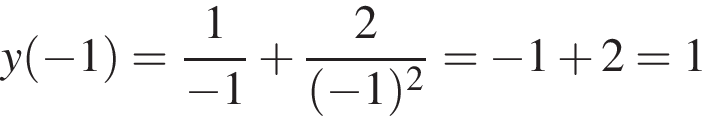
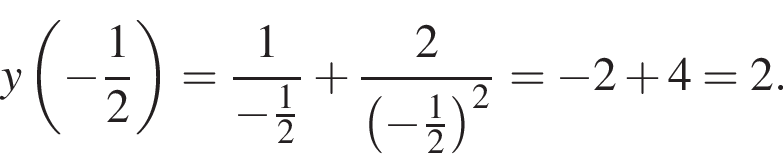
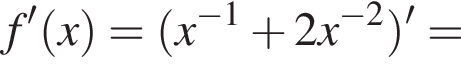
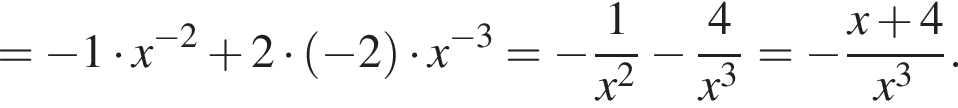
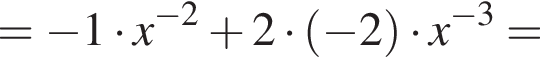
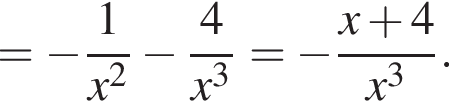
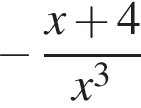 имеет только корень −4, при этом
имеет только корень −4, при этом 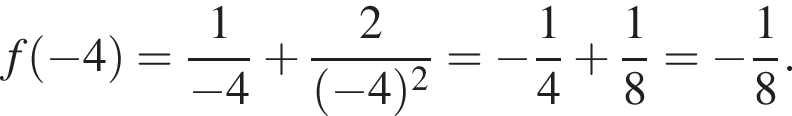
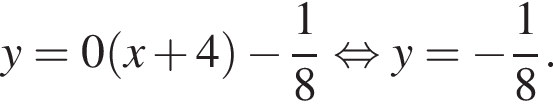
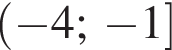 и отрицательно на отрезке
и отрицательно на отрезке 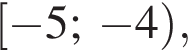 значит, исходная функция возрастает на
значит, исходная функция возрастает на 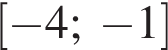 и убывает на
и убывает на 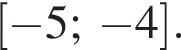 Поэтому наименьшее значение у нее
Поэтому наименьшее значение у нее 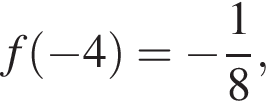 а наибольшее достигается в одном из концов отрезка:
а наибольшее достигается в одном из концов отрезка: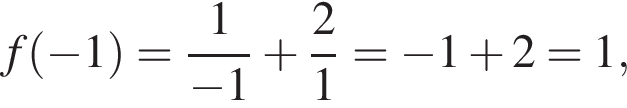
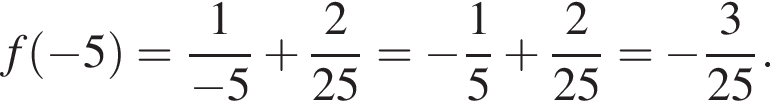
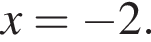 Функия определена на всем отрезке, вертикальных асимптот не имеет. Монотонность ее была уже исследована раннее. Осталась выпуклость. Возьмем вторую производную.
Функия определена на всем отрезке, вертикальных асимптот не имеет. Монотонность ее была уже исследована раннее. Осталась выпуклость. Возьмем вторую производную.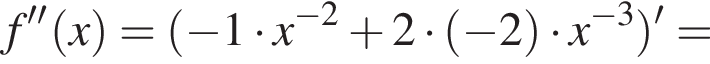
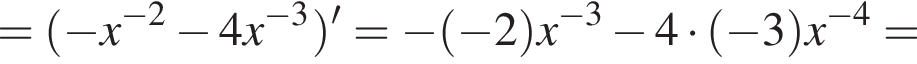
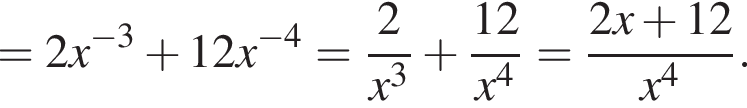
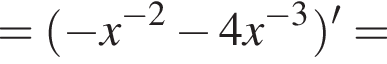
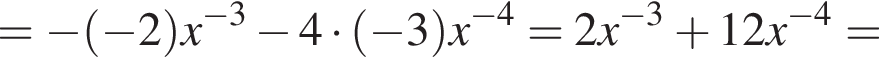
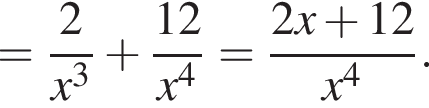
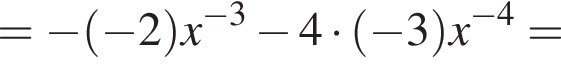
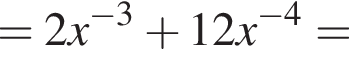

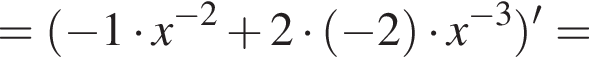
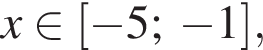 поэтому функция выпукла вверх. Осталось построить график.
поэтому функция выпукла вверх. Осталось построить график. 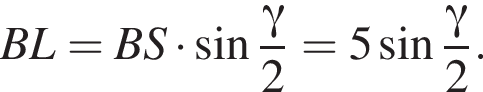
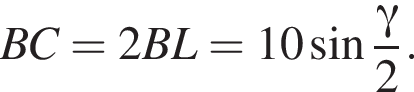 Найдём площадь равностороннего треугольника, лежащего в основании:
Найдём площадь равностороннего треугольника, лежащего в основании: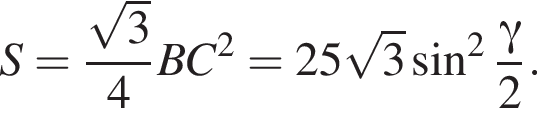
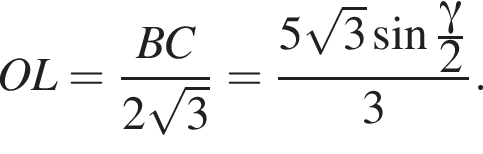 Апофема треугольника BSC равна
Апофема треугольника BSC равна 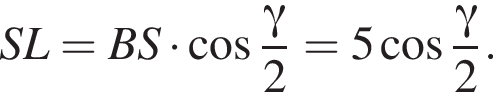
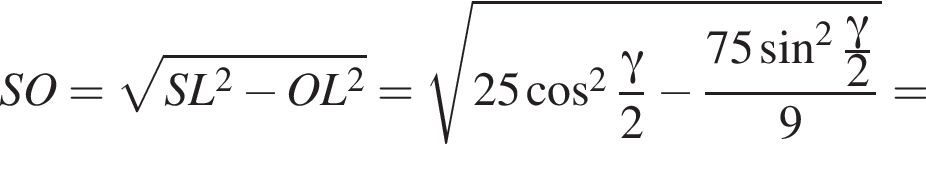
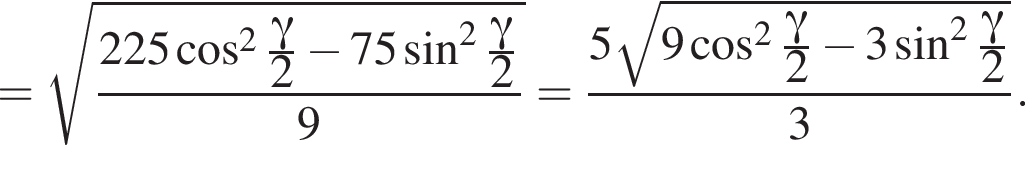
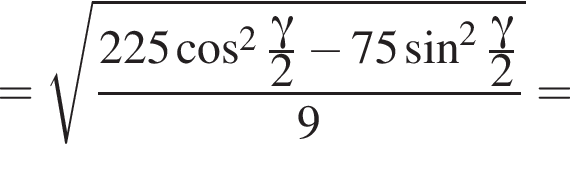
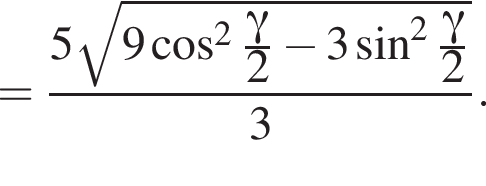

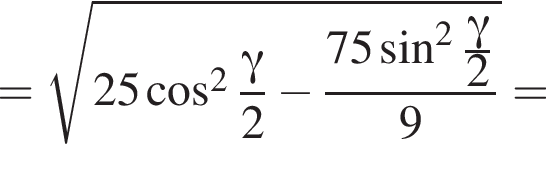
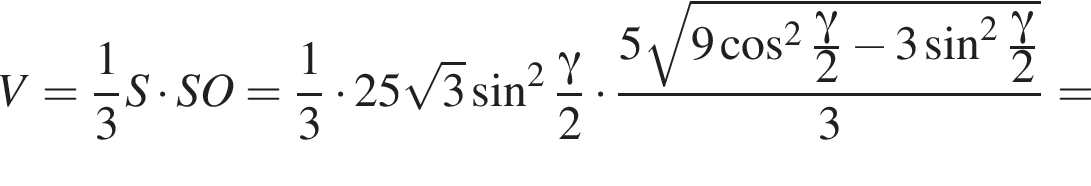
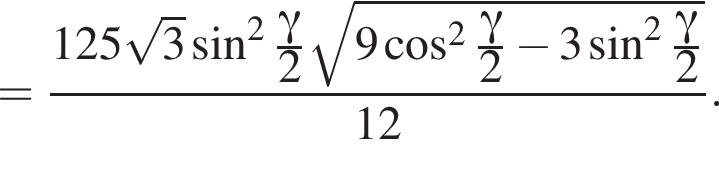
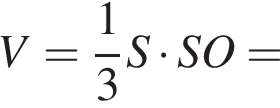
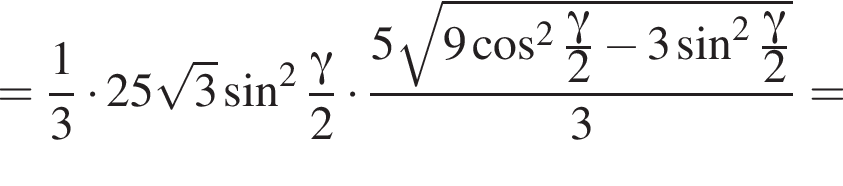
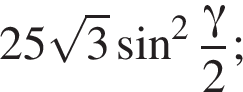 3)
3) 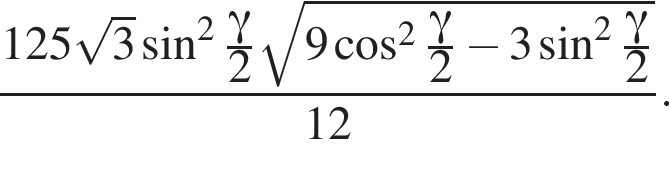
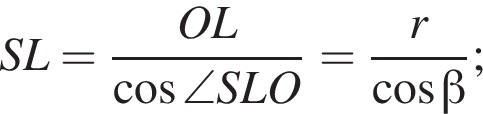

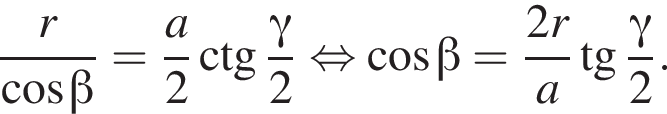
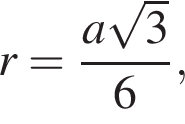 следовательно,
следовательно,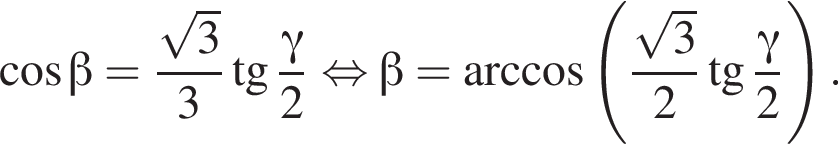
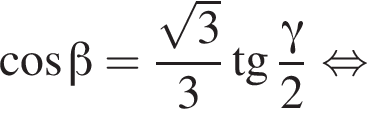
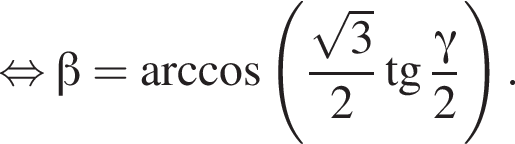
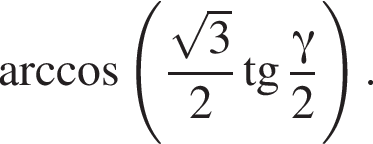
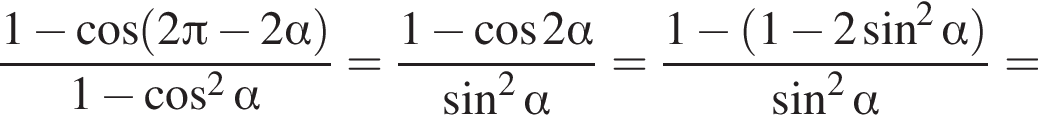
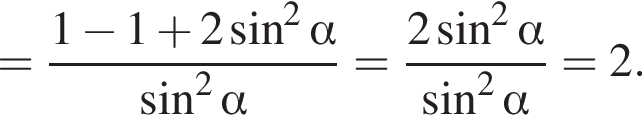
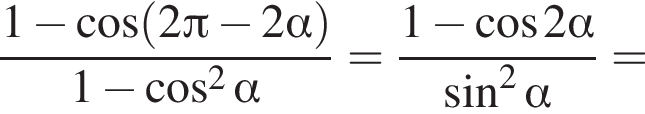
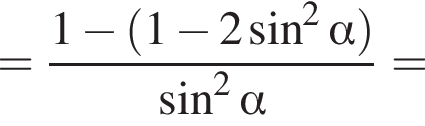
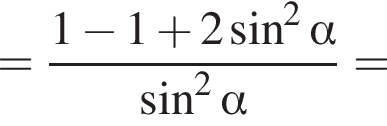
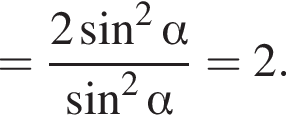
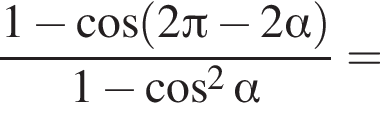
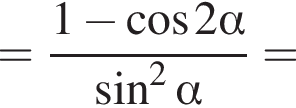
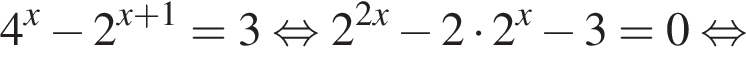
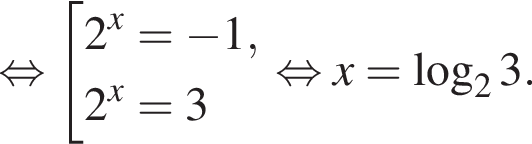
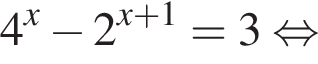
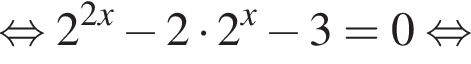
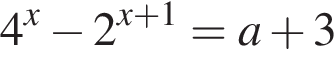 (*) должно иметь корни, ровно два из которых удовлетворяют неравенству
(*) должно иметь корни, ровно два из которых удовлетворяют неравенству 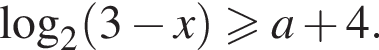
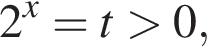
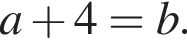 Тогда уравнение (*) принимает вид
Тогда уравнение (*) принимает вид 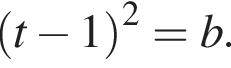 Это уравнение имеет два различных положительных корня
Это уравнение имеет два различных положительных корня 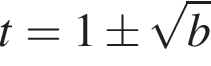 при
при 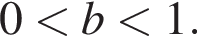 Таким образом,
Таким образом, 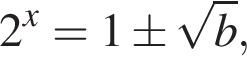 откуда
откуда 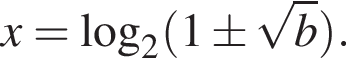 Так как
Так как  а
а 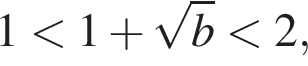 то
то  а
а 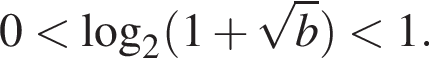
 при
при 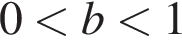 выполнено для всех
выполнено для всех 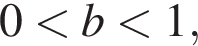 откуда
откуда