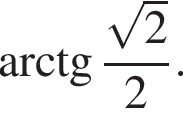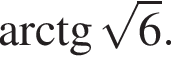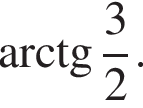Відповідно до умови завдання 31 (№ 3439) основою піраміди є квадрат, одне з бічних ребер перпендикулярно до площини основи. Площина бічної грані, що не проходить через висоту піраміди, нахилена до поверхні під кутом 45°. Найбільше бічне ребро дорівнює 12 см.
а) Зобразіть цю піраміду та побудуйте лінійний кут двогранного кута між бічними гранями, що не проходять через висоту піраміди.
б) Знайдіть цей кут.

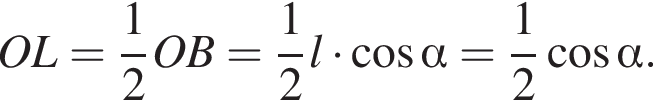
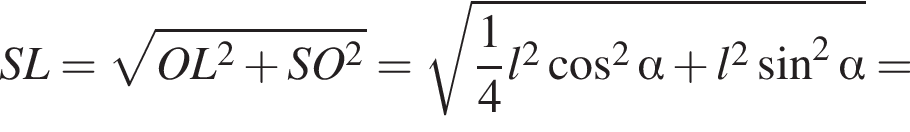
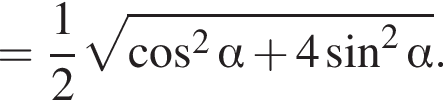

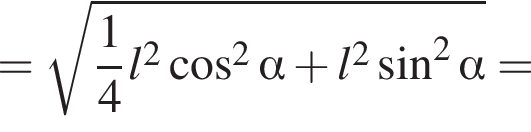
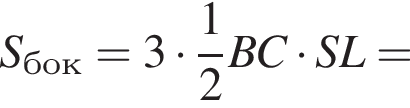
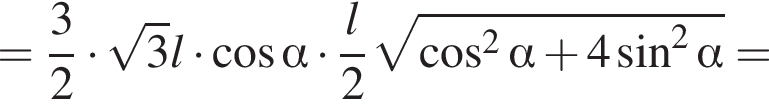
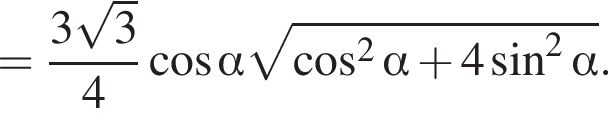

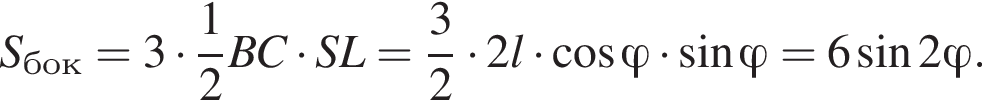
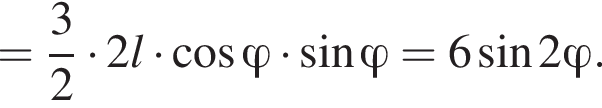
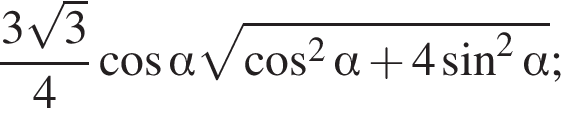 2)
2) 
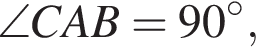

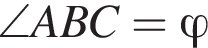 і кожне бічне ребро складає з площиною основи кут
і кожне бічне ребро складає з площиною основи кут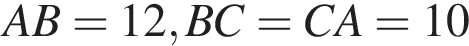 і двогранні кути при основі рівні
і двогранні кути при основі рівні