1. Тип 7 № 1045 

Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
Перетворення виразів. Прості перетворення
i
Спростіть вираз 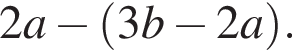
А) 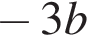
Б) 

В) 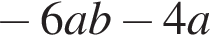
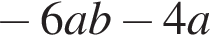
Г) 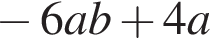
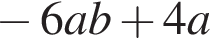
Д) 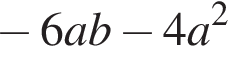
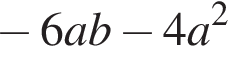
Решение. Упростим:
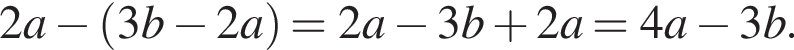
Правильный ответ указан под номером 2.
Ответ: 2
1045
2
Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
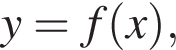 визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.
визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.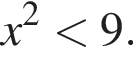
 Если подставить в неравенство остальные числа — они не подойдут.
Если подставить в неравенство остальные числа — они не подойдут.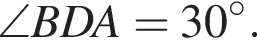
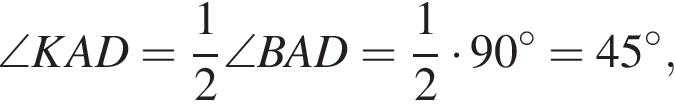
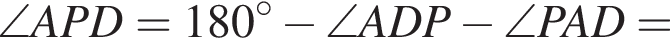


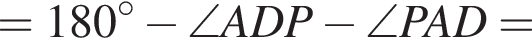
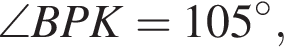 поскольку углы
поскольку углы 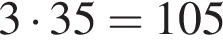 гривен, покупатель получает 4 шоколадки. Значит за
гривен, покупатель получает 4 шоколадки. Значит за  гривен он получит 8 шоколадок, а на оставшиеся 10 гривен ни одной шоколадки купить не сможет.
гривен он получит 8 шоколадок, а на оставшиеся 10 гривен ни одной шоколадки купить не сможет.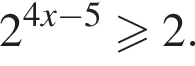
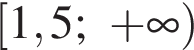
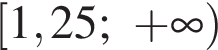


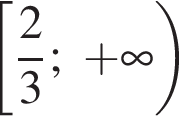
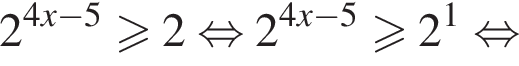
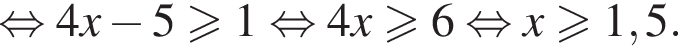
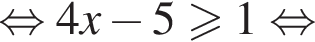

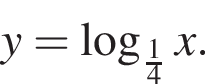
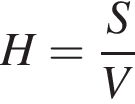
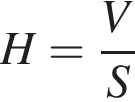
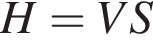
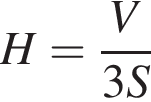
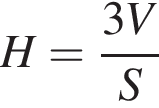
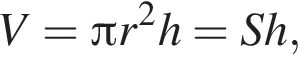 откуда
откуда 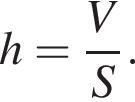
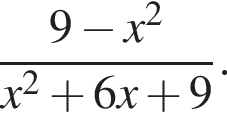
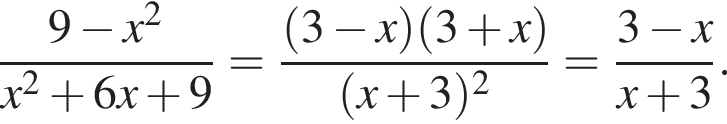
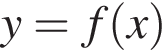 паралельно перенесли вздовж осі x на 2 одиниці праворуч. Графік якої з наведених функцій отримали?
паралельно перенесли вздовж осі x на 2 одиниці праворуч. Графік якої з наведених функцій отримали?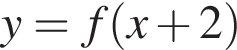
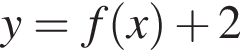
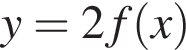
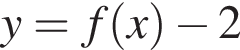
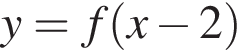
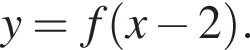
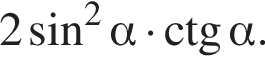

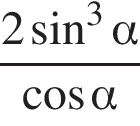
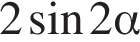
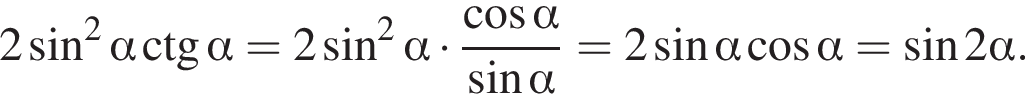
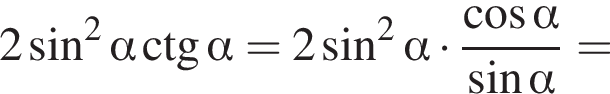

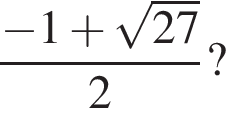
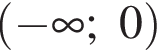

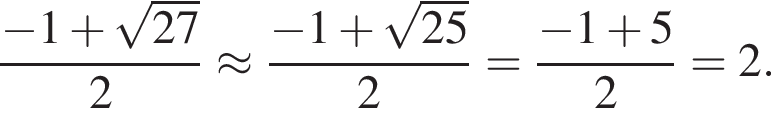
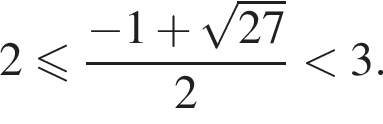 Заметим, что
Заметим, что  поэтому
поэтому 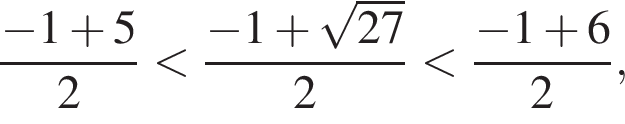
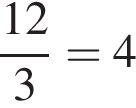 см
см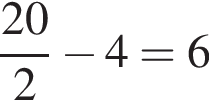 см
см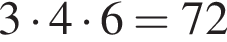 см2
см2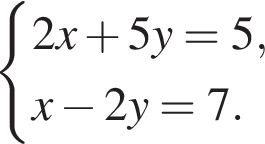
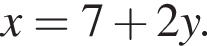 Подставляя в первое, находим
Подставляя в первое, находим 
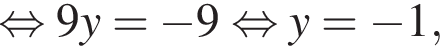


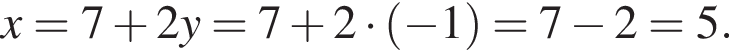

 та
та 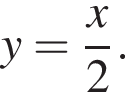 Укажіть формулу для обчислення площі зафарбованої фігури.
Укажіть формулу для обчислення площі зафарбованої фігури.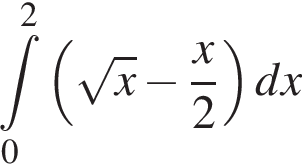
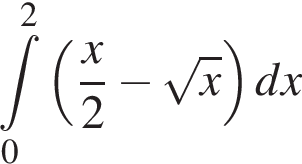
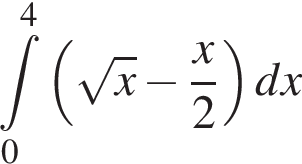
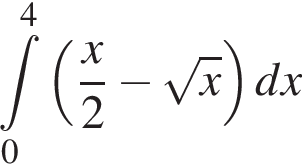
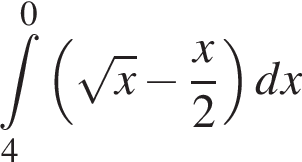
 идет выше графика
идет выше графика 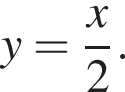 Значит, верная формула это
Значит, верная формула это 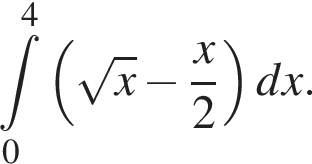
 Тоді KL = 0,6 м, LP = 1?6 м. Світлофор установлено на висоті h = 4,6 м над дорогою. Укажіть з-поміж наведених найменшу відстань d від точки A до точки P місця зупинки автобуса, за якої світлофор повністю потраплятиме в поле зору водія.
Тоді KL = 0,6 м, LP = 1?6 м. Світлофор установлено на висоті h = 4,6 м над дорогою. Укажіть з-поміж наведених найменшу відстань d від точки A до точки P місця зупинки автобуса, за якої світлофор повністю потраплятиме в поле зору водія.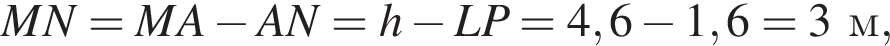
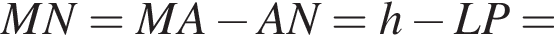
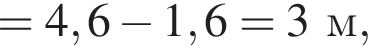
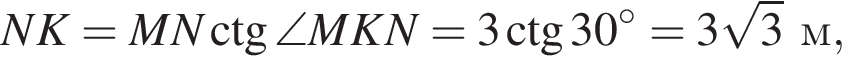

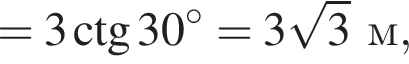
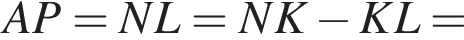
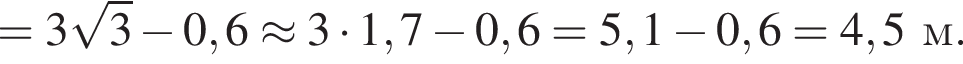
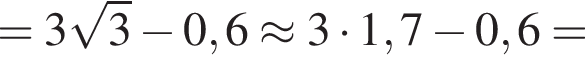
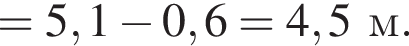
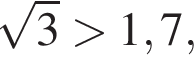 то
то 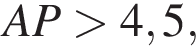 то есть
то есть 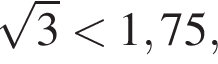 поэтому
поэтому 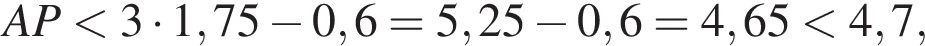
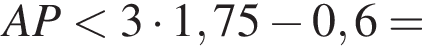
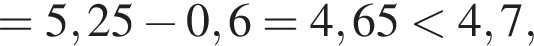
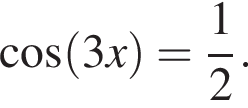
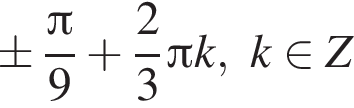
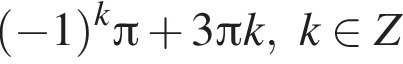

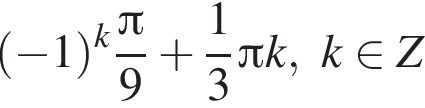
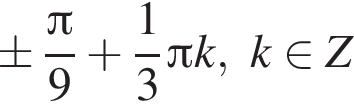
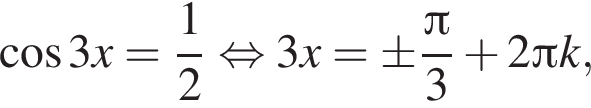
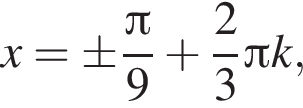
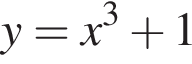
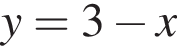


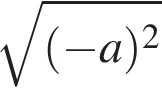
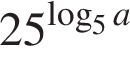
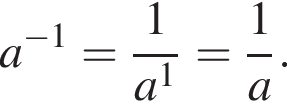 Получаем: 1 — Б.
Получаем: 1 — Б.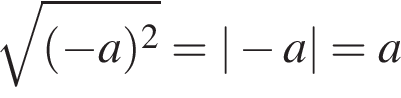 при
при 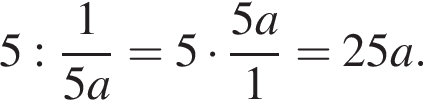 Получаем: 3 — Д.
Получаем: 3 — Д. 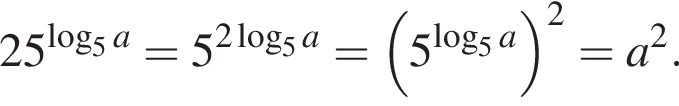
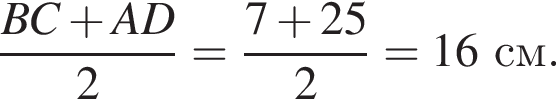
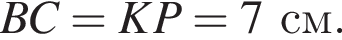 Найдем длину AK:
Найдем длину AK: 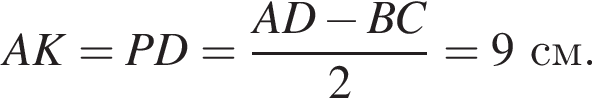
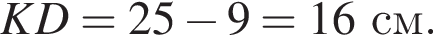

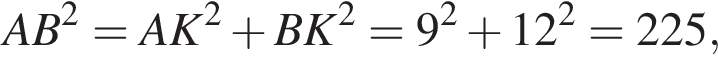
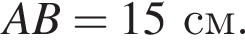
 Итак, 1 — Б.
Итак, 1 — Б. Таким образом, 2 — А.
Таким образом, 2 — А. Прямая BA — проекция AC на плоскость ABA1,
Прямая BA — проекция AC на плоскость ABA1,
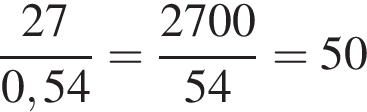



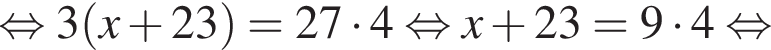
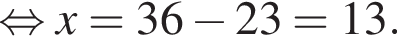
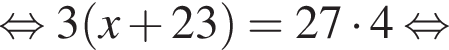
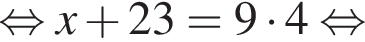
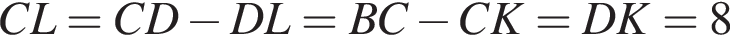 см
см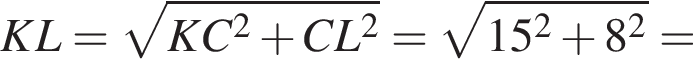
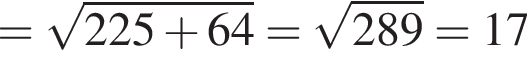

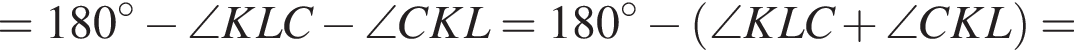

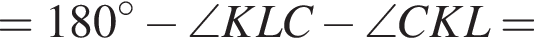

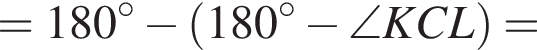
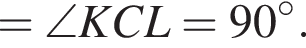
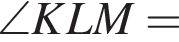
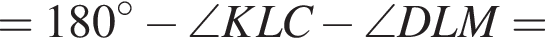
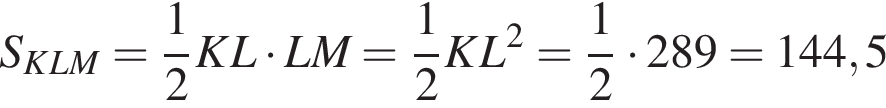
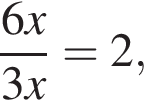 знаменатель прогрессии равен 2. В таком случае и
знаменатель прогрессии равен 2. В таком случае и 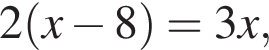 откуда
откуда 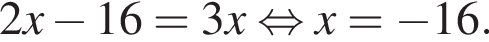
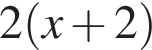 километра, а против течения
километра, а против течения 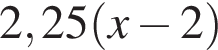 километра. По условию
километра. По условию 
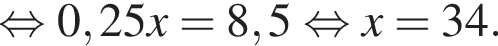
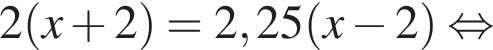
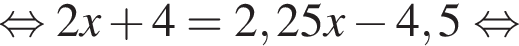
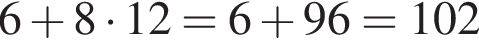 варианта.
варианта.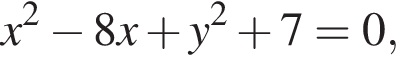 збігається з точкою перетину діагоналей AC i BD паралелограма ABCD. Обчисліть площу цього паралелограма, якщо A(−4; −3) i B(0; 3).
збігається з точкою перетину діагоналей AC i BD паралелограма ABCD. Обчисліть площу цього паралелограма, якщо A(−4; −3) i B(0; 3).
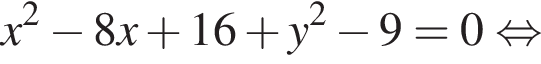
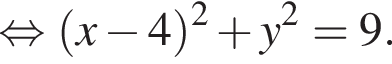
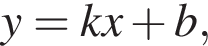 тогда
тогда  и
и  откуда
откуда 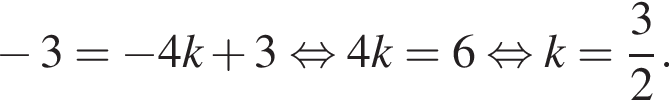
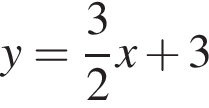 или
или 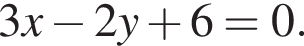
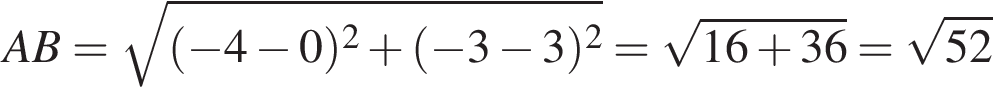
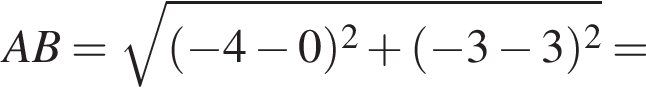
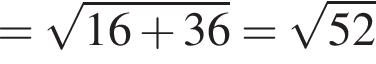
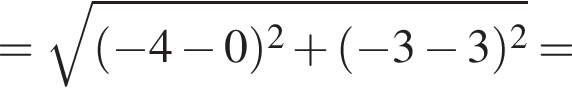
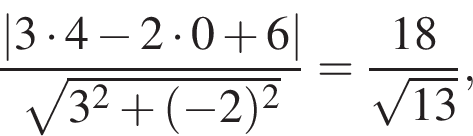
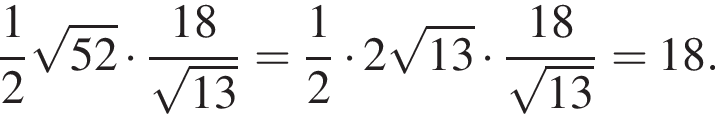

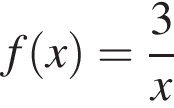 i
i 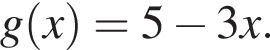
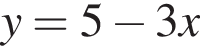 — прямая, проходящая через точки
— прямая, проходящая через точки 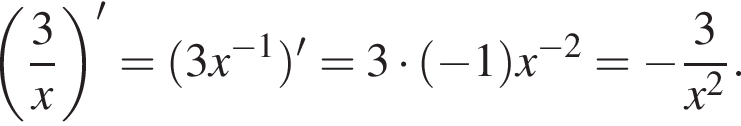
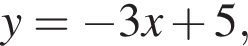 если их коэффициенты при x в уравнении будут равны −3. Угловой коэффициент касательной равен значению производной в точке касания, остается решить уравнение
если их коэффициенты при x в уравнении будут равны −3. Угловой коэффициент касательной равен значению производной в точке касания, остается решить уравнение 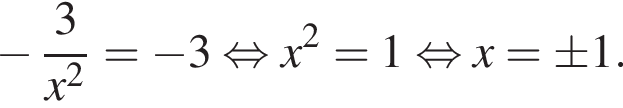
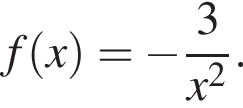
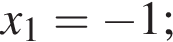

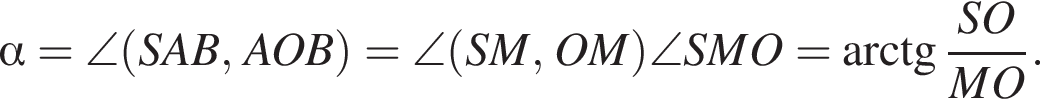
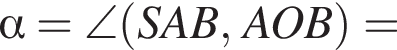
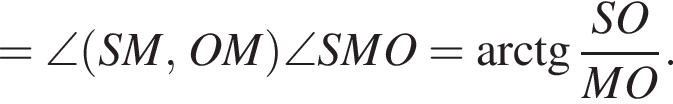

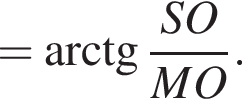
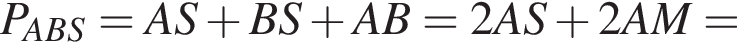
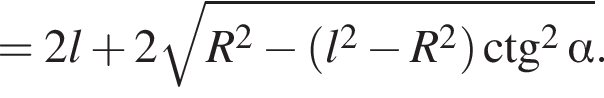

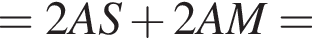
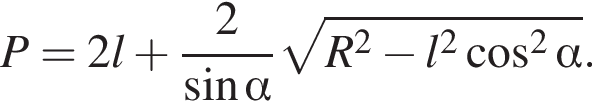
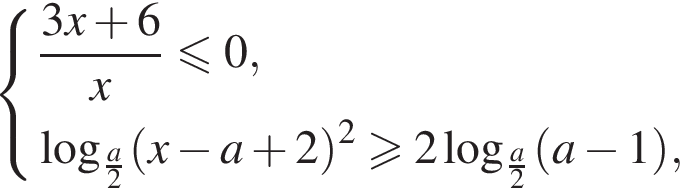
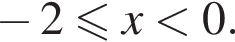 Во втором неравенстве сразу заметим, что
Во втором неравенстве сразу заметим, что 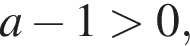 и
и 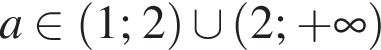 — при прочих a неравенство не определено ни при одном значении x. При таких a сразу преобразуем неравенство к виду
— при прочих a неравенство не определено ни при одном значении x. При таких a сразу преобразуем неравенство к виду 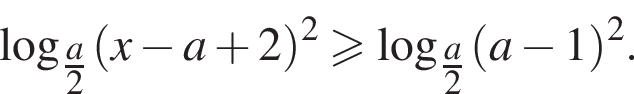
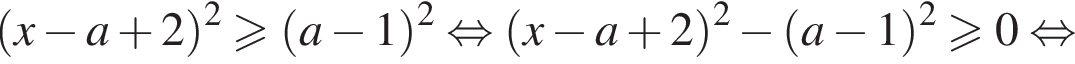


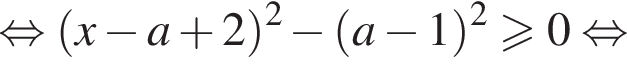
 получим
получим  При
При 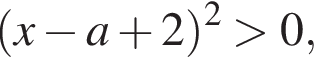 то есть
то есть 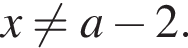 В первом случае дополнительное условие было не нужно, поскольку
В первом случае дополнительное условие было не нужно, поскольку 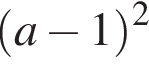 всегда положительно при
всегда положительно при 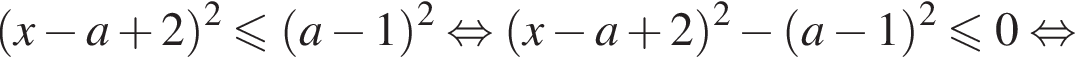

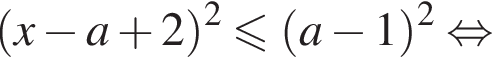
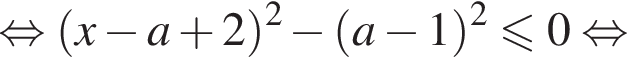
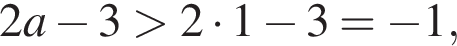 получим
получим  Число
Число 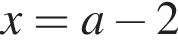 точно лежит в этом промежутке и его нужно исключить.
точно лежит в этом промежутке и его нужно исключить.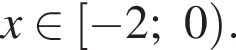
 якщо
якщо 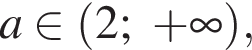
 якщо
якщо 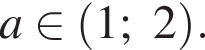
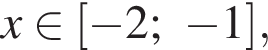 якщо
якщо  якщо
якщо 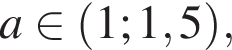
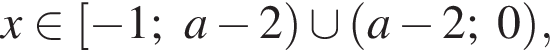 якщо
якщо