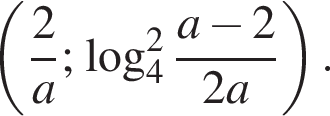На діаграмі відображено обсяг видобутку алмазів (у млн карат) у 2006 році в п’яти країнах Африки. Користуючись діаграмою, визначте країни Африки, у кожній з яких маса алмазів, видобутих у 2006 році, більш ніж удвічі перевищувала масу алмазів, видобутих у цьому році в Анголі.
Система навігації, вбудована в спинку літакового крісла, повідомляє пасажира про те, що політ проходить на висоті 34 000 футів. Виразіть висоту польоту в метрах. Вважайте, що 1 фут дорівнює 30,5 см.
У правильній чотирикутній піраміді всі ребра дорівнюють 1. Знайдіть площу перерізу піраміди площиною, що проходить через середини бічних ребер.
Знайдіть корінь рівняння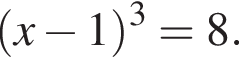
У рівнобедреному трикутнику ABC з основою AC
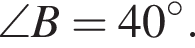 Визначте градусну міру кута А.
Визначте градусну міру кута А.
На рисунку зображено графік функції
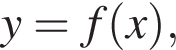 визначеної на проміжку' [−3; 2]. Укажіть точку перетину графіка функції
визначеної на проміжку' [−3; 2]. Укажіть точку перетину графіка функції 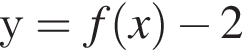 з віссю y.
з віссю y.
Спростіть вираз 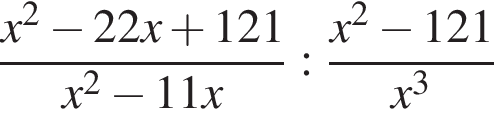 .
.
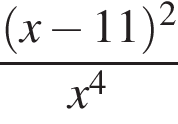
З формули доцентрового прискорення a = ω 2 R знайдіть R (у метрах), якщо ω = 4 с −1 та a = 64 м/с 2 .
Якому з наведених проміжків належить число 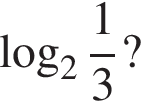
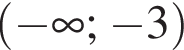

Які з наведених тверджень є правильними?
I. Через точку, що не лежить на даній прямій можна провести не більше однієї прямої, паралельної даної.
II. Через точку, що лежить на даній прямій можна провести нескінченну безліч прямих, перпендикулярних даної прямої.
III. Кожен відрізок має певну довжину, більшу нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-який його точкою.
Розв’яжіть рівняння 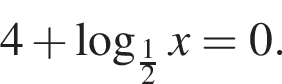
Знайдіть похідну функції 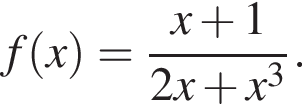
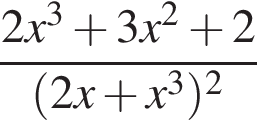
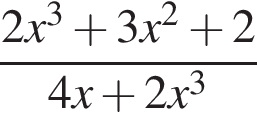
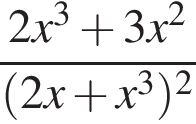
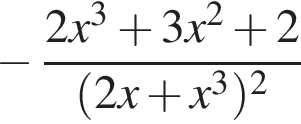
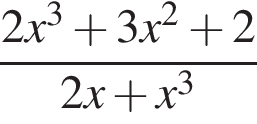
Розв’яжіть систему нерівностей: 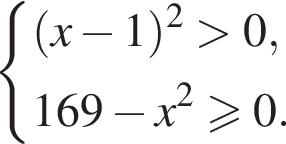
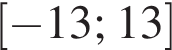
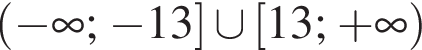
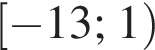
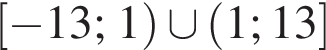
Знайдіть значення виразу
У правильній чотирикутній піраміді висота дорівнює 12, об’єм дорівнює 200. Знайдіть бічне ребро цієї піраміди.
На рисунку зображено осьовий переріз світлодіодної лампи. Активна поверхня цієї лампи, через яку відбувається випромінювання світла, є тілом обертання, утвореним обертанням відрізка AB та чверті кола BC навколо осі l. Використовуючи зазначені на рисунку дані, обчисліть площу активної поверхні світлодіодної лампи. Виберіть відповідь, найближчу до точної.
Співвіднесіть функцію (1-3) та її властивості (А-Д):
1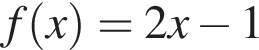
2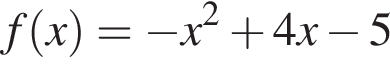
3
А функція є періодичною
Б графік функції має вигляд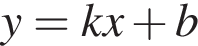
У функція досягає максимуму в точці (2; 0)
Г графік функції проходить через точку початку координат
Д функція досягає максимуму в точці (2; −1)
Установіть відповідність між виразом (1–3) та проміжком (А–Д), якому належить його значення.
1 ![]()
2 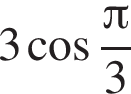
3 
А 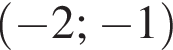
Б 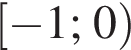
В ![]()
Г ![]()
Д ![]()
На рисунку зображено п’ять прямокутників (А−Д) та зазначено довжини їхніх сторін.
1. площа прямокутника дорівнює 48
2. периметр прямокутника дорівнює 14
3. кут між діагоналями прямокутника дорівнює 60°
4. діагональ прямокутника дорівнює 14
Установіть відповідність між геометричним тілом (1−4) та площею його повної поверхні (А−Д).
1. конус з радіусом основи 3 та твірною 5
2. циліндр з радіусом основи 3 та висотою 4
3. куля радіуса ![]()
4. куб з ребром ![]()
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Мобільний телефон у магазині коштує 2260 грн. Покупець не має можливості заплатити всю суму повністю, тому купує цей телефон у розстрочку. За умовою договору він має сплачувати 10% від його ціни кожен місяць протягом 12 місяців з моменту купівлі.
1. Визначте щомісячний платіж за куплений у розстрочку телефон (у грн).
2. Знайдіть суму 12 щомісячних платежів. На скільки гривень ця сума перевищує заявлену магазином ціну телефона (2260 грн) на момент купівлі.
У паралелограмі АВСD з вершини тупого кута В проведено висоти ВK та ВМ (див. рисунок). ВK = 16 см, AK = 12 см, ВМ = 24 см.
1. Визначте довжину сторони АВ (у см).
2. Обчисліть площу (у см2) паралелограма АBСD.
У прямокутній системі координат у просторі задано вектор 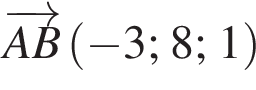 і точку
і точку 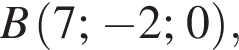 точка О — початок координат.
точка О — початок координат.
1. Визначте ординату y точки 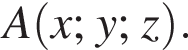
2. Обчисліть скалярний добуток 
Другий член арифметичної прогресії (an) на 7,2 більший за її шостий член.
1. Визначте різницю d цієї прогресії.
2. Визначте перший член a1 цiєї прогресії, якщо 
Маша колекціонує принцес із Кіндер-сюрпризів. Всього в колекції 10 різних принцес і вони рівномірно розподілені, тобто в кожному черговому Кіндер-сюрпризі може з рівними ймовірностями виявитися будь-яка з 10 принцес. Маша вже має дві різні принцеси з колекції. Яка ймовірність того, що для отримання наступної принцеси Маші доведеться купити ще 2 або 3 шоколадні яйця?
Залізничний потяг довжиною в 1 км пройшов би повз стовп за 1 хв., а через тунель (від входу локомотива до виходу останнього вагона) за тієї ж швидкості — за 3 хв. Яка довжина тунелю (км)?
Обчисліть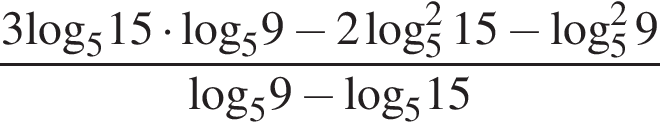 .
.
Розв'яжіть рівняння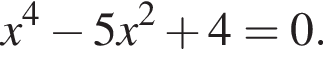 У відповідь запишіть добуток усіх його дійсних коренів.
У відповідь запишіть добуток усіх його дійсних коренів.
Марійка зірвала на клумбі 9 нарцисів та 4 тюльпани. Скільки всього існує способів вибору із цих квітів 3 нарцисів та 2 тюльпанів для букета?
Задано функцію 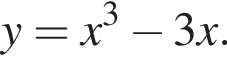
| x | y |
|---|---|
| 0 | |
| −1 | |
| 2 |
1. Для наведених у таблиці значень аргументи х визначте відповідні їм значення у (див. таблиця).
2. Визначте й запишіть координати точок перетину графіка функції 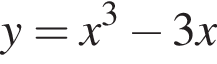 із віссю x.
із віссю x.
3. Знайдіть похідну f' функції 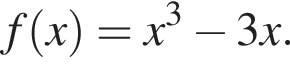
4. Визначте нулі функції f'.
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції f.
6. Побудуйте ескіз графіка функції f.
Апофема правильної трикутної піраміди дорівнює 2. Плоский кут при вершині дорівнює γ.
а) Зобразіть на малюнку цю піраміду та кут γ.
б) Знайдіть площу бічної поверхні піраміди.
в) Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3532) висота правильної чотирикутної піраміди дорівнює 3. Бічні грані нахилені до основи під
1. Зобразіть на малюнку цю піраміду і побудуйте кут між боковим ребром та основою.
2. Знайдіть цей кут.
Доведіть тотожність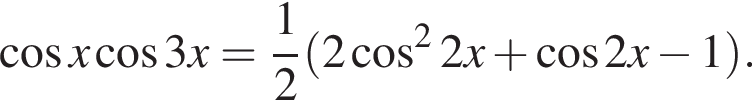
Задано систему рівнянь
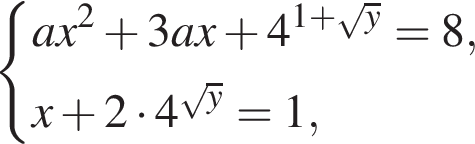
де x, y — змінні, a — довільна стала.
1. Розв’яжіть систему, якщо ![]()
2. Визначте всі розв’язки заданої системи залежно від значень a.

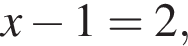 откуда
откуда 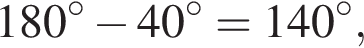 значит,
значит, 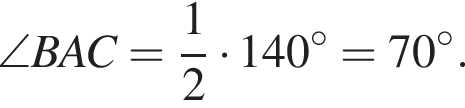
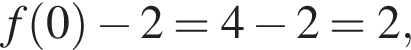 точкой пересечения будет (0; 2). То, что
точкой пересечения будет (0; 2). То, что  видно из графика f(x).
видно из графика f(x).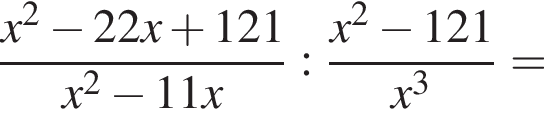
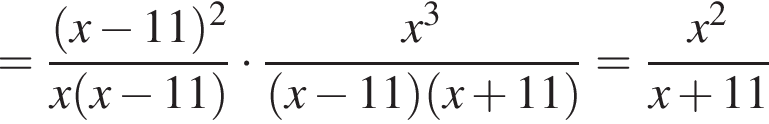
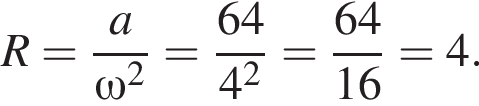
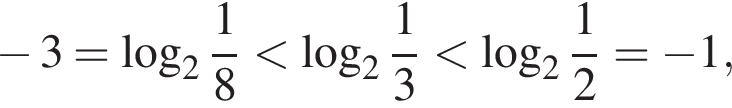
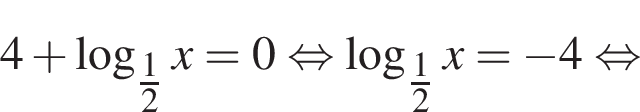
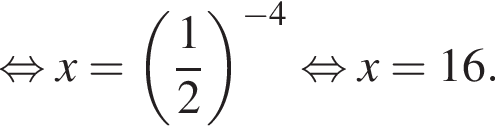
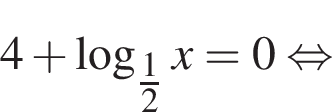
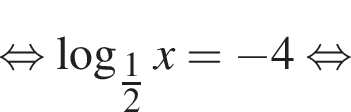
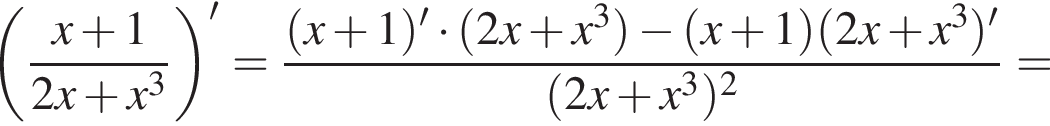
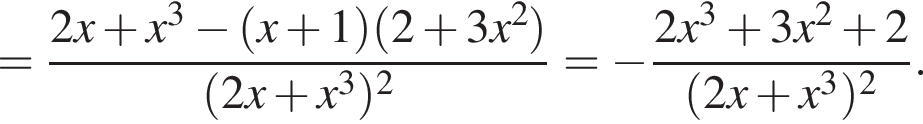
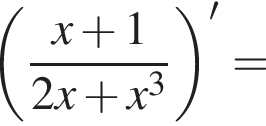
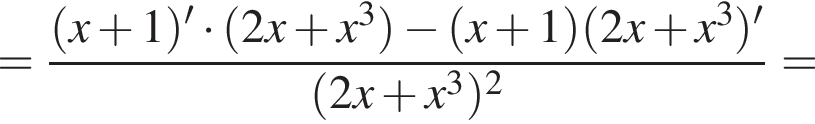
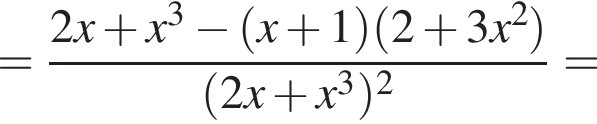
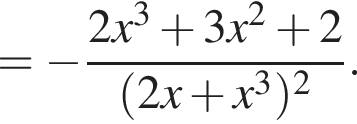
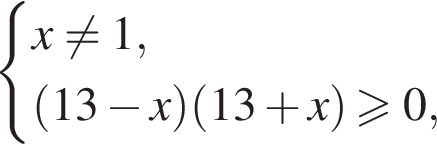
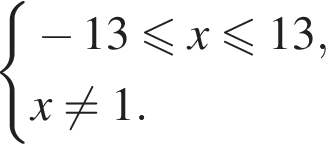
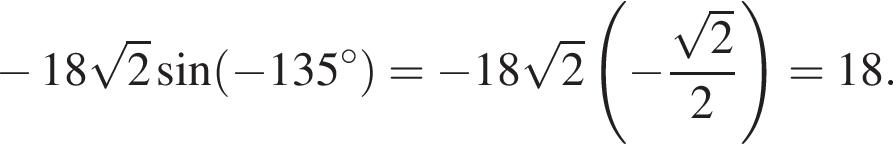
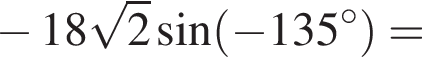
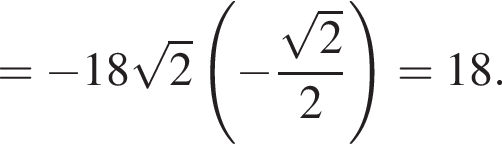
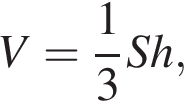 откуда площадь основания
откуда площадь основания 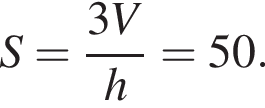 Сторона основания тогда
Сторона основания тогда  а диагональ
а диагональ 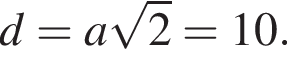 Боковое ребро найдем по теореме Пифагора:
Боковое ребро найдем по теореме Пифагора: 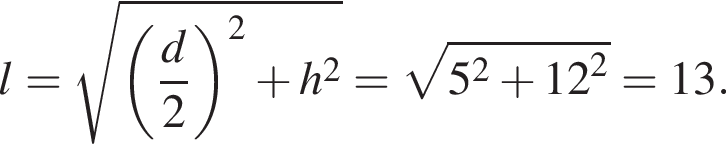
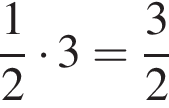 см,
см, 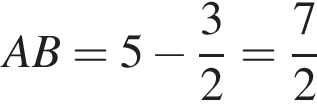 см. Площадь боковой поверхности цилиндра равна
см. Площадь боковой поверхности цилиндра равна 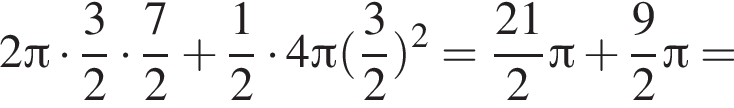
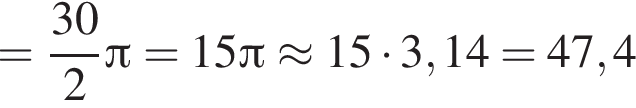
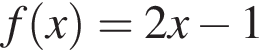 имеет вид
имеет вид 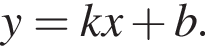 Ответ — Б.
Ответ — Б.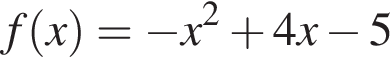 достигает максимума в точке (2; −1). Ответ — Д.
достигает максимума в точке (2; −1). Ответ — Д. является периодической. Ответ — А.
является периодической. Ответ — А.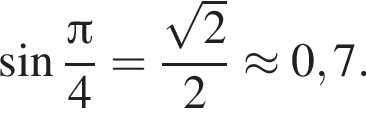 Данное значение соответствует промежутку
Данное значение соответствует промежутку 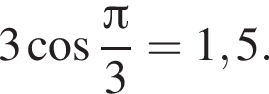 Данное значение соответствует промежутку
Данное значение соответствует промежутку  Данное значение соответствует промежутку
Данное значение соответствует промежутку 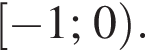 Ответ — Б.
Ответ — Б.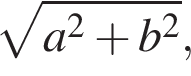 где a и b — соседние стороны. Только
где a и b — соседние стороны. Только 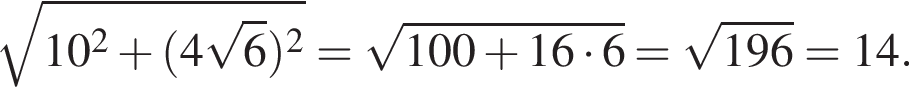
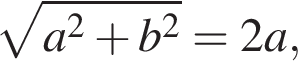 откуда
откуда 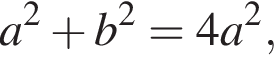
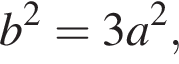
 Это верно только для прямоугольника
Это верно только для прямоугольника 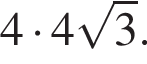

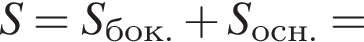
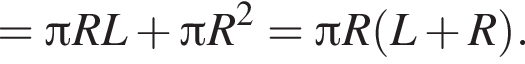
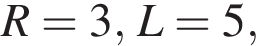 то
то  Следовательно, 1 — Б.
Следовательно, 1 — Б. 

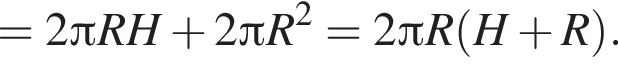
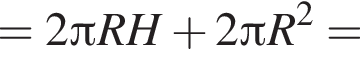

 тогда
тогда 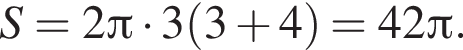 Итак, 2 — Г.
Итак, 2 — Г. 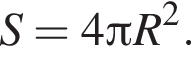 По условию
По условию 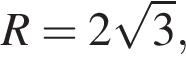 тогда
тогда 
 можно вычислить по формуле
можно вычислить по формуле 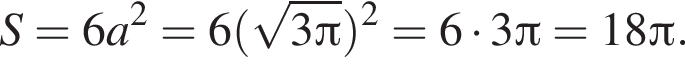
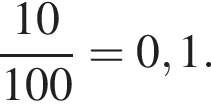 Получаем:
Получаем: 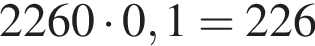 гривен.
гривен. гривны.
гривны.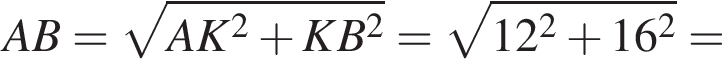

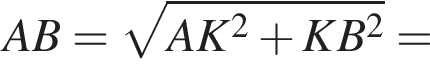
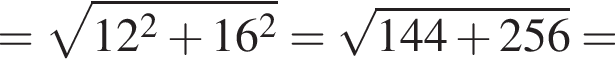
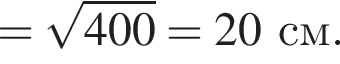
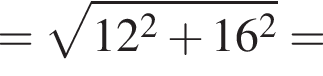
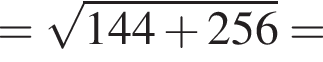
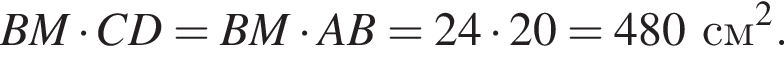
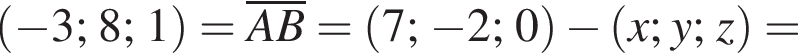
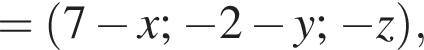
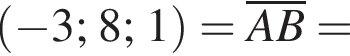
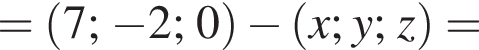
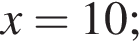
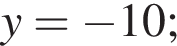
 Найдем произведение векторов:
Найдем произведение векторов: 
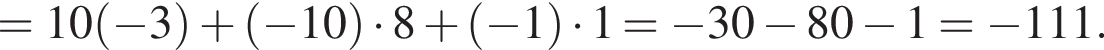

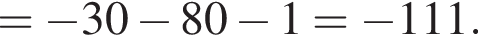
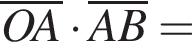
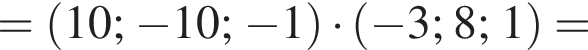
 тогда
тогда 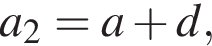
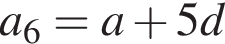 и по условию
и по условию 
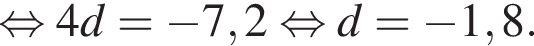
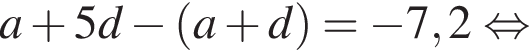
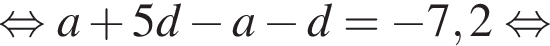
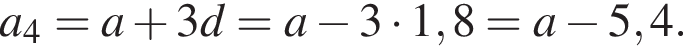
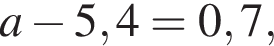 откуда
откуда 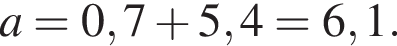
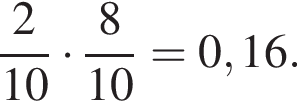 Вероятность того, что для получения следующей принцессы Маше придётся купить 3 шоколадных яйца, равна
Вероятность того, что для получения следующей принцессы Маше придётся купить 3 шоколадных яйца, равна 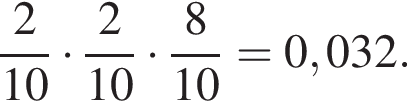 Таким образом, искомая вероятность — 0,16 + 0,032 = 0,192.
Таким образом, искомая вероятность — 0,16 + 0,032 = 0,192.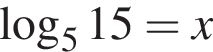 и
и 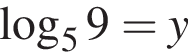 . Тогда упростим:
. Тогда упростим: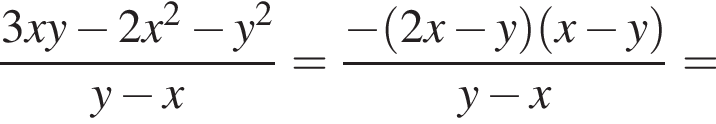
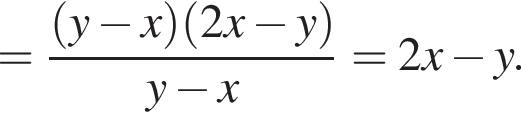
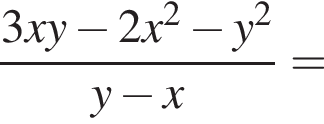
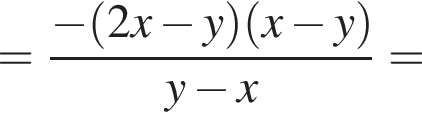
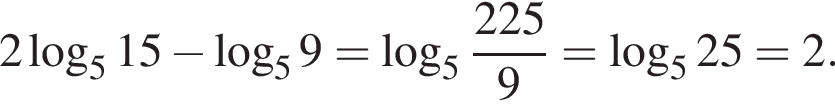

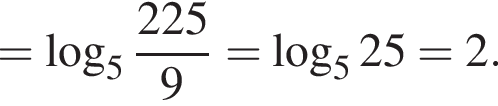
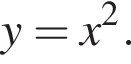 Получаем уравнение
Получаем уравнение 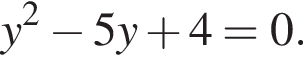 Корни:
Корни: 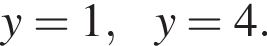 Если
Если 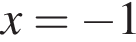 или
или 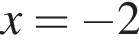 или
или 
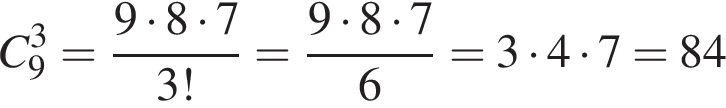
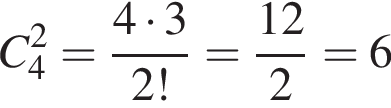 способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно
способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно 
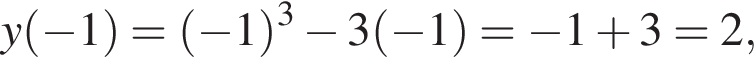
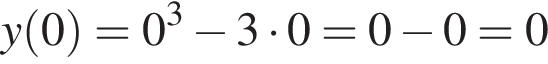
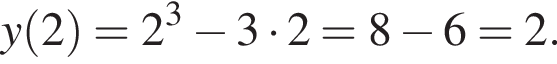
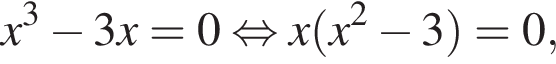 откуда
откуда 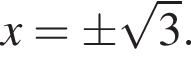 Возьмем производную функции:
Возьмем производную функции: 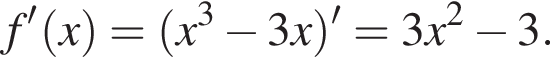
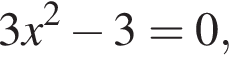 получим
получим 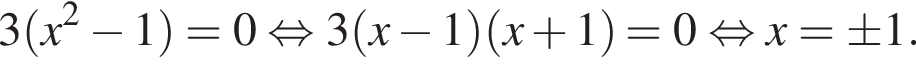
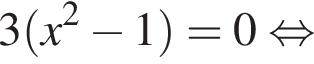
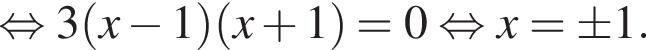
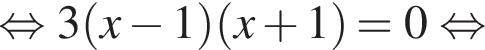

 и при
и при  (функция убывает). При
(функция убывает). При 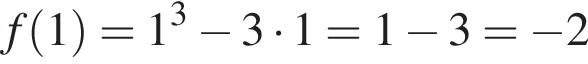
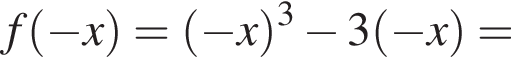
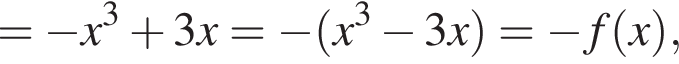
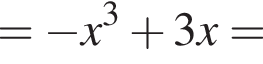
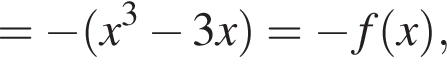
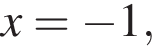 то
то 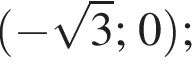
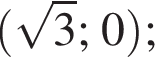
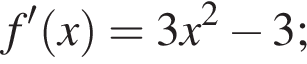


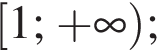 проміжок спадання: [−1; 1]; точки екстремуму:
проміжок спадання: [−1; 1]; точки екстремуму: 
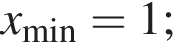 екстремуми:
екстремуми: 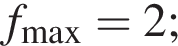

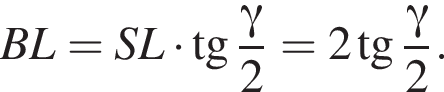
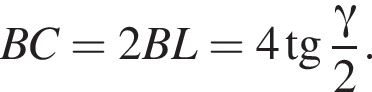 Найдём площадь полной поверхности пирамиды:
Найдём площадь полной поверхности пирамиды: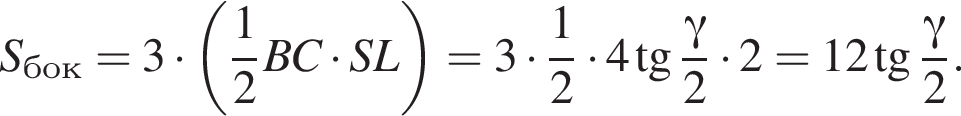
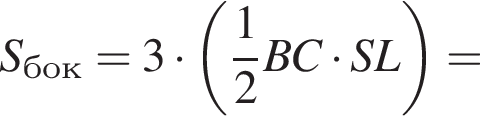
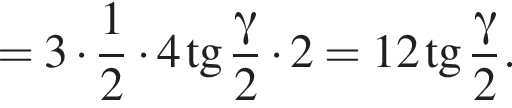
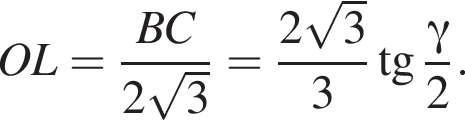 Высоту пирамиды SO найдем по теореме Пифагора:
Высоту пирамиды SO найдем по теореме Пифагора: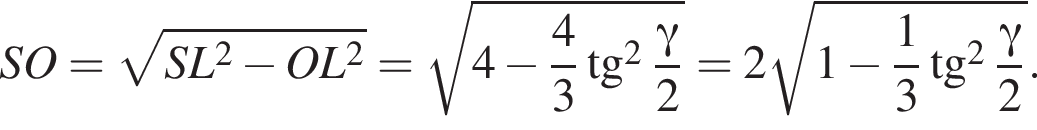

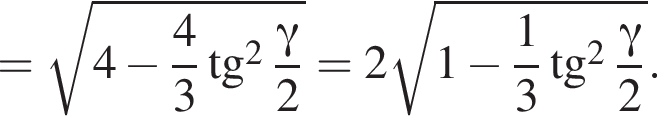
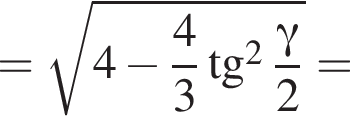
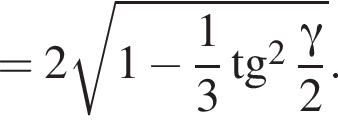
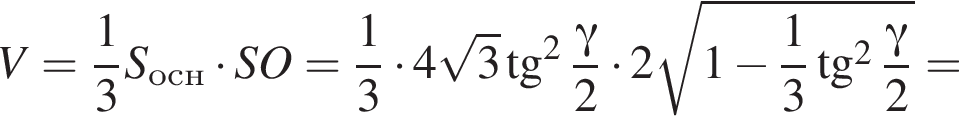
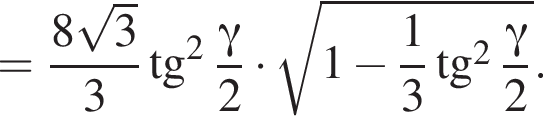
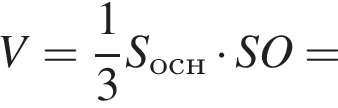
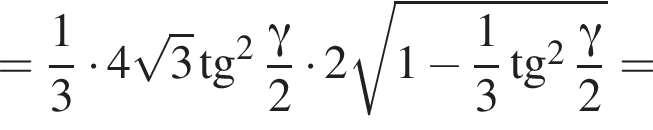
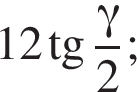 3)
3) 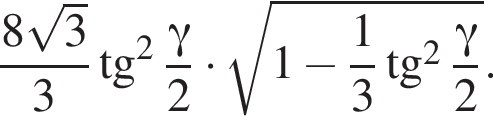

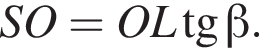
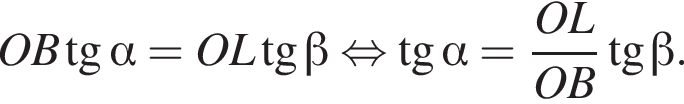
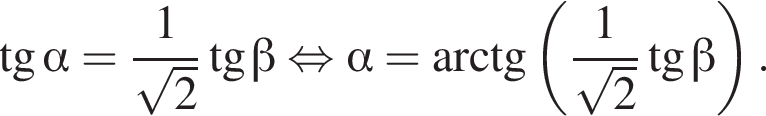
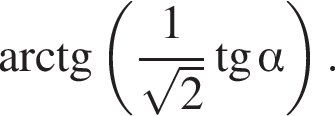
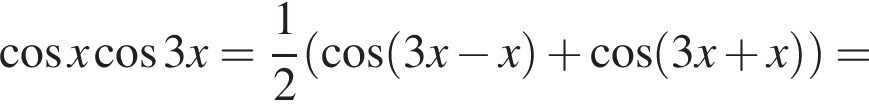
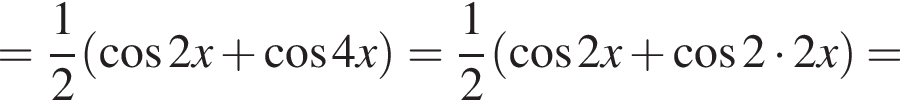
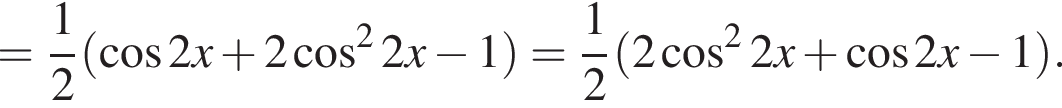
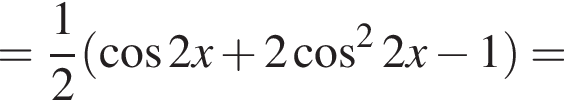
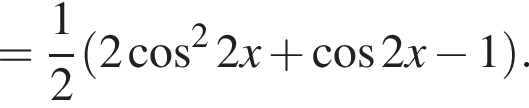
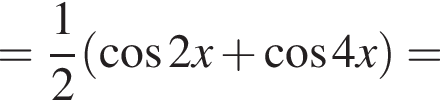
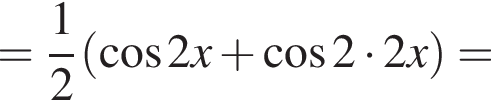

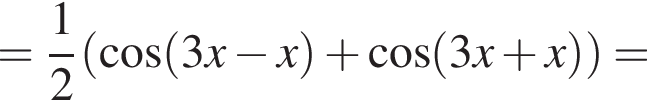
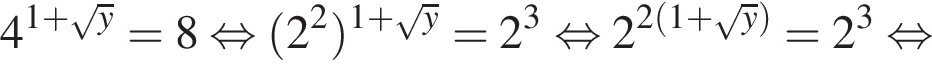
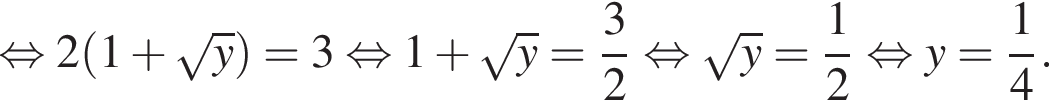
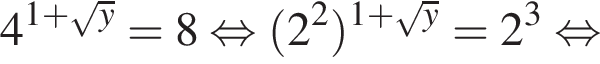

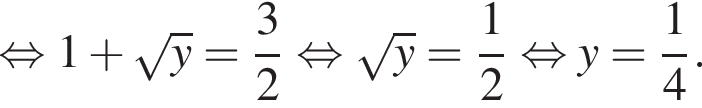
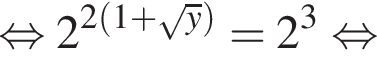
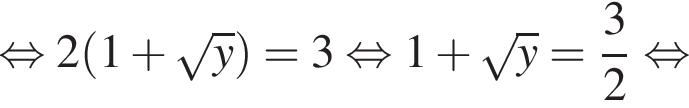
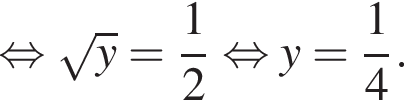
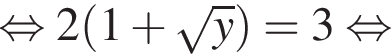
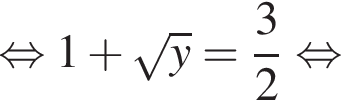
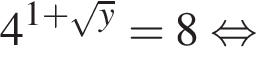
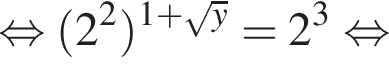
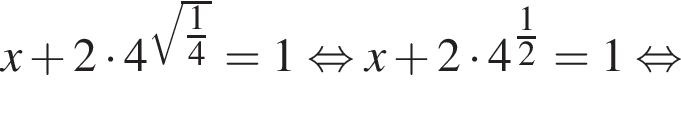
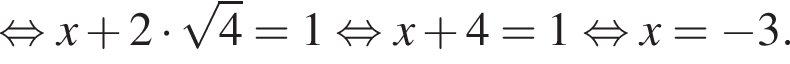
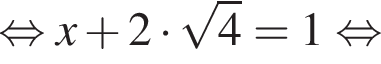
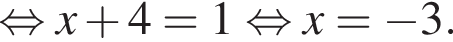
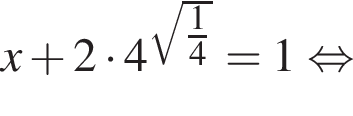
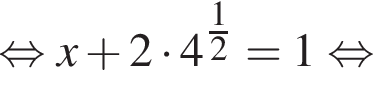

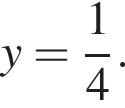

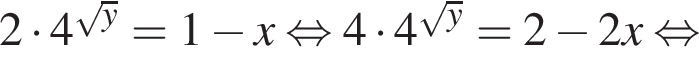
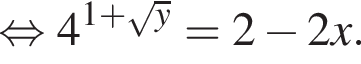


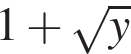 принимает все значения из промежутка
принимает все значения из промежутка  поэтому
поэтому 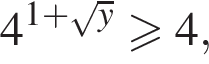
 и
и  Используем равенство
Используем равенство  в первом уравнении. Получим
в первом уравнении. Получим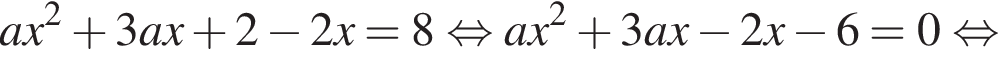

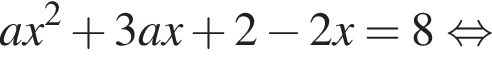
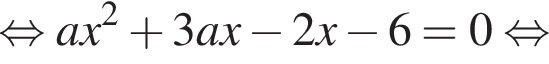
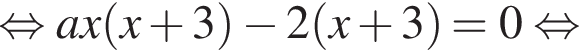
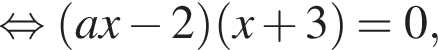
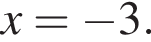 Если
Если 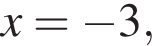 то
то 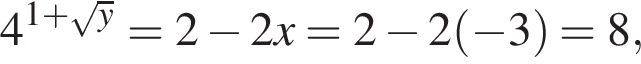
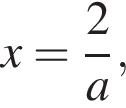 причем
причем 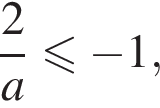 то
то 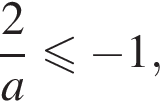 откуда
откуда 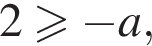
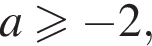 то есть
то есть 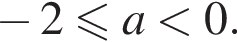 При таких a получаем
При таких a получаем 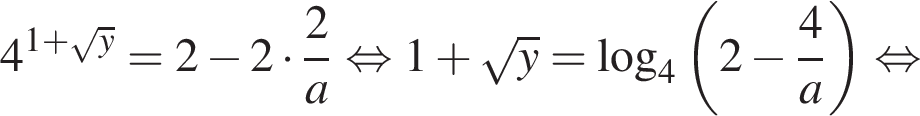
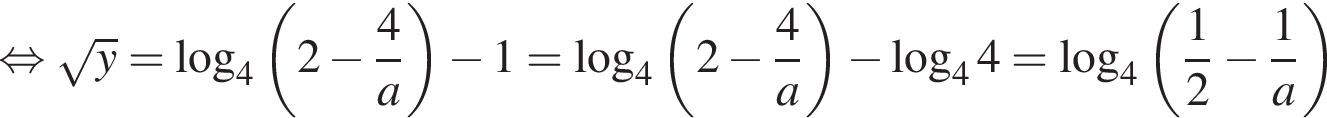
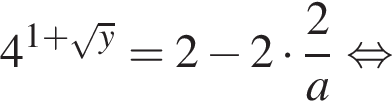
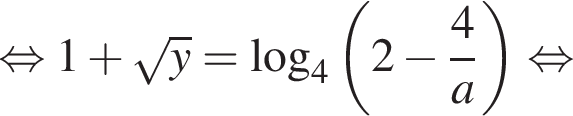
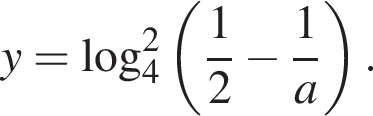 Это выражение определено, поскольку это гарантировано условием
Это выражение определено, поскольку это гарантировано условием 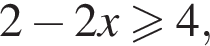 о котором мы позаботились. Есть еще отдельный случай, когда
о котором мы позаботились. Есть еще отдельный случай, когда 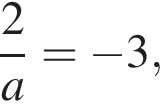 то есть
то есть 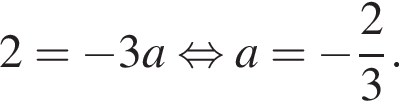 В этом случае найденные решения совпадают.
В этом случае найденные решения совпадают.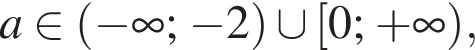 то розв'язком системи є (−3; 0,25); якщо
то розв'язком системи є (−3; 0,25); якщо 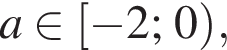 то розв'язками системи є (−3; 0,25)
то розв'язками системи є (−3; 0,25)