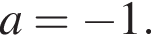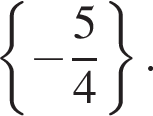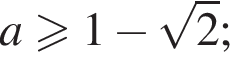На рисунку зображено графік залежності шляху S (у км), пройденого групою туристів, від часу t (у год). Яке з наведених тверджень є правильним?
Відстань між Києвом та Стокгольмом дорівнює 1265 км. Округліть її до сотень кілометрів.
Знайдіть об’єм піраміди, зображеної на малюнку. Її основою є багатокутник, сусідні сторони якого перпендикулярні, а одне з бічних ребер перпендикулярно площині основи
Знайдіть корінь рівняння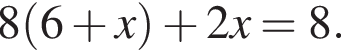
Прямі a і b перетинаються, утворюють чотири кути. Відомо, що сума трьох кутів дорівнює 220°. Знайдіть градусну міру меншого кута.
На рисунку зображено графік функції
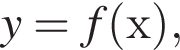 визначеної на проміжку [−4; 6]. Укажіть найбільшв значення функції f на цьому проміжку.
визначеної на проміжку [−4; 6]. Укажіть найбільшв значення функції f на цьому проміжку.
Спростіть вираз 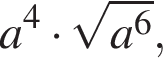 де
де ![]()
Площу трикутника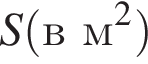 можна обчислити за формулою
можна обчислити за формулою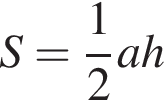 , де a – сторона трикутника, h – висота, проведена до цієї сторони (в метрах). Користуючись цією формулою, знайдіть сторону
, де a – сторона трикутника, h – висота, проведена до цієї сторони (в метрах). Користуючись цією формулою, знайдіть сторону![]() якщо площа трикутника дорівнює
якщо площа трикутника дорівнює![]() , А висота h дорівнює 14 м.
, А висота h дорівнює 14 м.
Укажіть проміжок, якому належить значення виразу 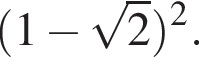
Яке з наступних тверджень є вірним?
I. Точка дотику двох кіл рівновіддалена від центрів цих кіл.
ІІ. У паралелограмі є два рівні кути.
ІІІ. Площа прямокутного трикутника дорівнює добутку довжин його катетів.
Розв'яжіть систему рівнянь
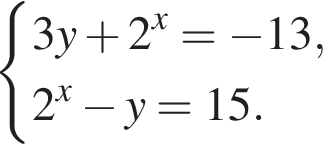
Якщцо (x0; y0) — розв'язок цієї системи, To 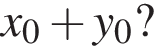
Функція 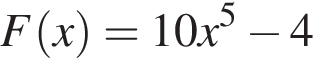 є первісною функції f(х). Укажіть функцію G(х), яка також є первісною функції f(х).
є первісною функції f(х). Укажіть функцію G(х), яка також є первісною функції f(х).
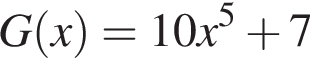
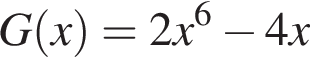


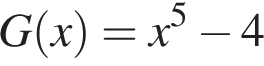
Розв’яжіть систему нерівностей: 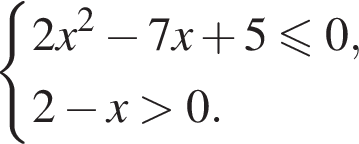
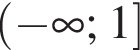
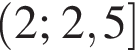
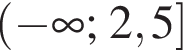
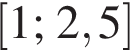
Спростiть вираз 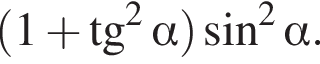
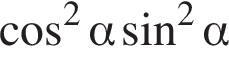
Периметр основи правильної трикутної призми дорівнює 12 см, а периметр її бічної грані — 20 см. Визначте площу бічної поверхні призми.
На кресленні кутової шафи (вид зверху) зображено рівні прямокутники ABCD i KMEF та п'ятикутник EMOAD (див. рисунок). Визначте довжину відрізка ED, якщо
 м,
м, м
м м.
м.
Установіть відповідність між графіком (1−3) функції, визначеної на проміжку [−4; 4], та її властивістю (А−Д).
А функція є непарною
Б найменше значення функції на проміжку [1; 3] дорівнює 2
В функція є парною
Г графік функції не має спільних точок із графіком рівняння 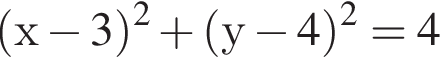
Д графік функції тричі перетинає пряму у = 1
Увідповідніть вираз (1−3) із його значенням (А−Д), якщо 
1. 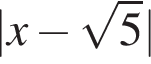
2. 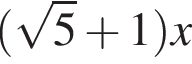
3. 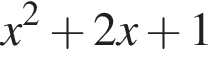
А −1
Б 1
В 4
Г 5
Д 6
На рисунку зображено коло із центром у точці O. Хорди AB і АС рівні. AK — діаметр. PM — дотична до кола, проведена в точці C,
 До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, шоб утворилося правильне твердження.
До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, шоб утворилося правильне твердження.
1. Градусна міра гула OCM дорівнює
2. Градусна міра кута ACP дорівнює
3. Градусна міра меншої дуги AB дорівнює
4. Градусна міра меншої дуги KC дорівнює
А 50°
Б 80°
В 90°
Г 100°
Д 120°
На рисунку зображено куб ABCDA1B1C1D1. До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
1. Пряма CB
2. Пряма CD1
3. Пряма AC
4. Пряма A1B
А паралельна площині AA1B1B
Б перпендикулярна до площини AA1B1B
В належить площині AA1B1B
Г має з площиною AA1B1B
Д утворює з площиною AA1B1B кут 45°
На виставці представлено лише два види мистецьких робіт: картини та скульптури, причому кількість скульптур у 4 рази менша за кількість картин.
1. Скільки відсотків становить кількість картин від загальної кількості робіт на виставці?
2. На скільки відсотків кількість картин більша за кількість скульптур?
На рисунку зображено ромб ABCD та коло, побудоване на меншій діагоналі BD як на діаметрі. Довжина кола дорівнює
![]() Це коло ділить діагональ AC на три відрізки AK, KM та MC, довжини яких відносяться як 1 : 6 : 1.
Це коло ділить діагональ AC на три відрізки AK, KM та MC, довжини яких відносяться як 1 : 6 : 1.
1. Обчислiть довжину дiфгоналi BD.
2. Визначте площу ромба ABCD.
В прямоугольной системе координат в пространстве задан вектор 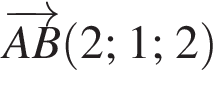 с началом в точке A(−1; −2; 3).
с началом в точке A(−1; −2; 3).
1. Найдите абсциссу точки B.
2. Вычислите модуль вектора 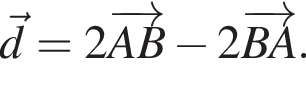
Геометрична прогресія задана умовою 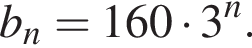
1. Найдите сумму первого члена этой прогрессии.
2. Знайдіть суму перших її 4 членів.
Біатлоніст п'ять разів стріляє по мішенях. Імовірність влучення в ціль при одному пострілі дорівнює 0,8. Знайдіть ймовірність того, що біатлоніст перші три рази потрапив у мішені, а останні два промахнувся. Результат округліть до сотих.
Андрій у понеділок, вівторок та п’ятницю витрачав по 16 грн на день, у середу й четвер — по 11 грн на день, у суботу — 35 грн, а в неділю грошей не витрачав.
Скільки гривень витрачав Андрій у середньому на день цього тижня?
Обчисліть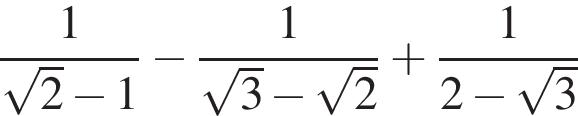 .
.
Розв'яжіть рівняння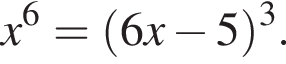 У відповідь запишіть суму всіх його дійсних коренів.
У відповідь запишіть суму всіх його дійсних коренів.
Олег пише смс-повідомлення з трьох речень. У кінці кожного з них він прикріпить один із п’ятнадцяти веселих смайликів. Скільки всього є способів вибору таких смайликів для прикріплення, якщо всі смайлики в повідомленні мають бути різними?
| x | y |
|---|---|
| −1 | |
| 0 | |
| 1 |
Задано функцію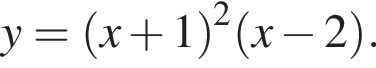
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення (див. таблицю).
2. Визначте та запишіть координати точок перетину графіка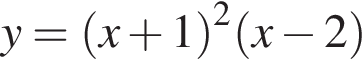 з віссю x .
з віссю x .
3. Знайдіть похідну f' функції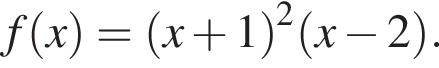 Визначте нулі функції f '.
Визначте нулі функції f '.
4. Визначте проміжки зростання та спадання, точки екстремуму функції f .
5. Побудуйте ескіз графіка функції f .
6. Знайдіть площу фігури, розташованої в третій координатній чверті та обмеженою графіком функції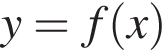 і прямою
і прямою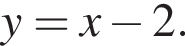
Апофема правильної трикутної піраміди дорівнює 5. Бічні ребра нахилені до основи під кутом α.
а) Зобразіть на малюнку цю піраміду та кут α.
б) Знайдіть площу бічної поверхні піраміди.
в) Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3506) Апофема правильної трикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під кутом α.
а) Зобразіть на малюнку цю піраміду та побудуйте двогранний кут при боковому ребрі.
б) Знайдіть цей кут.
Доведіть тотожність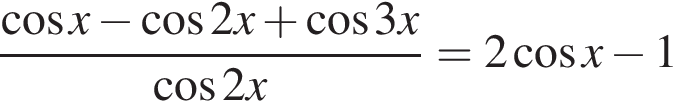
Задано рівняння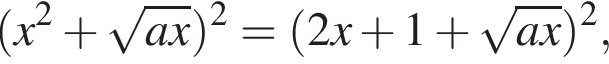 де x - Змінна; a – параметр.
де x - Змінна; a – параметр.
1. Розв'яжіть рівняння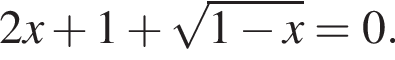
2. Знайдіть усі значення a , при кожному з яких рівняння має єдиний корінь на відрізку [−1; 1].

 при округлении до сотен получим 1300 км.
при округлении до сотен получим 1300 км.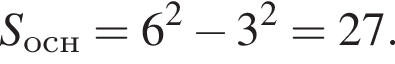
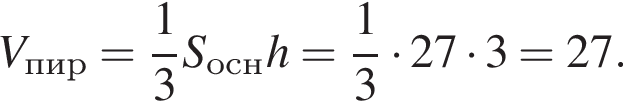
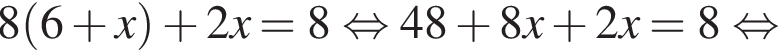

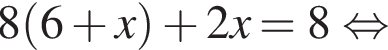

 равна 360°, поэтому четвертый угол равен 140°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 40°.
равна 360°, поэтому четвертый угол равен 140°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 40°. Значит,
Значит,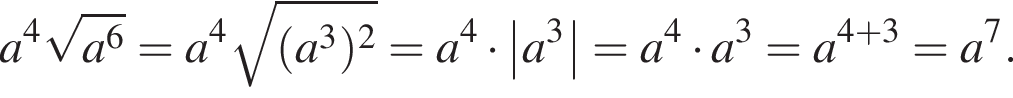
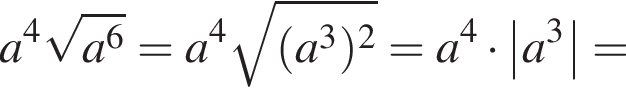
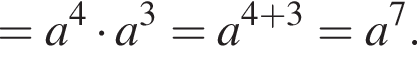
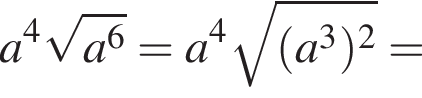
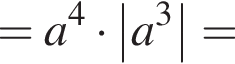
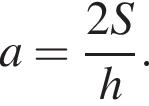
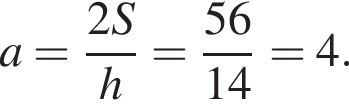
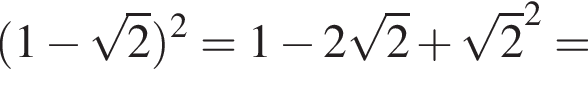


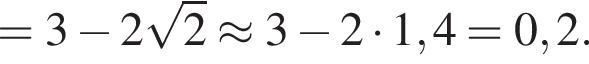
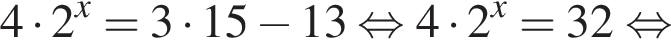
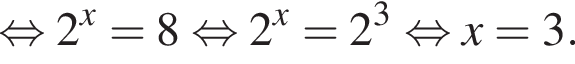
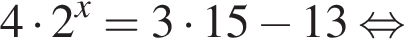
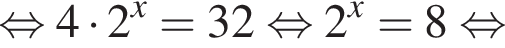
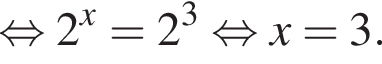
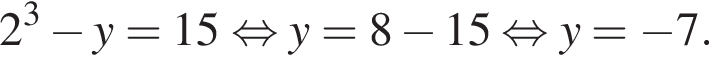 Значит
Значит 
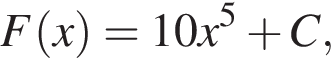 где С — произвольное число. Тогда:
где С — произвольное число. Тогда: 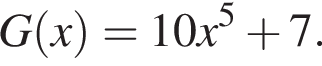
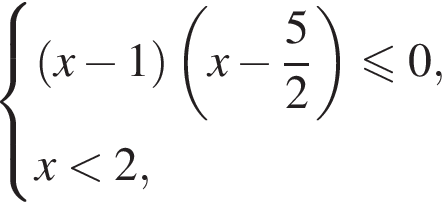
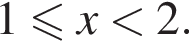
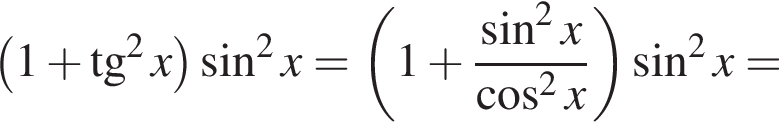
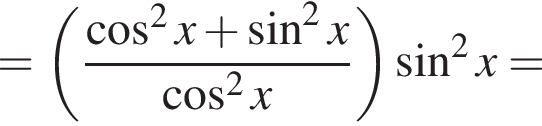
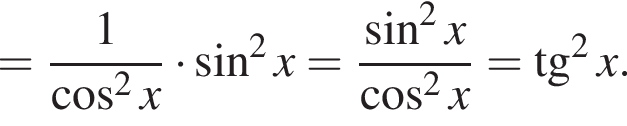
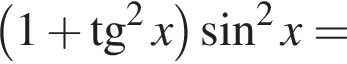
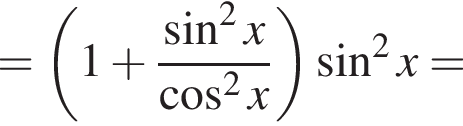
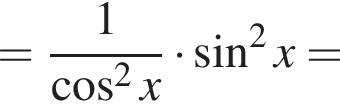
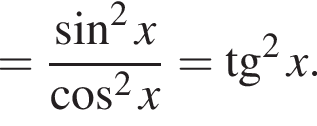
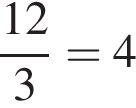 см
см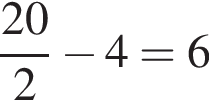 см
см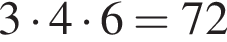 см2
см2
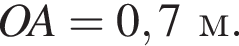 Мысленно продолжим AD и ME до пересечения в точке T, тогда OATM окажется квадратом. Тогда
Мысленно продолжим AD и ME до пересечения в точке T, тогда OATM окажется квадратом. Тогда 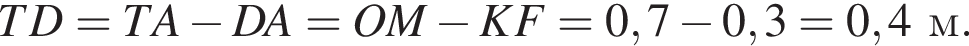
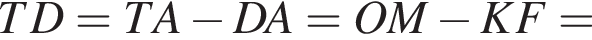
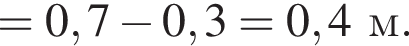
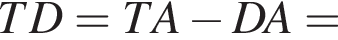

 м.
м.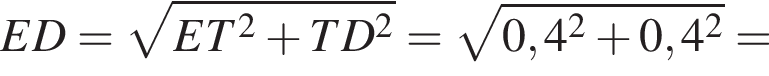
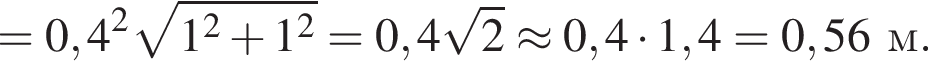

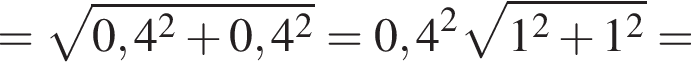
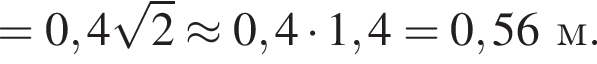
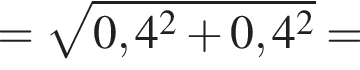
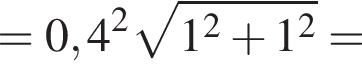
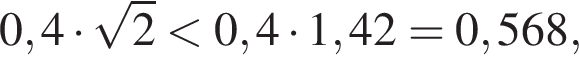 поэтому ошибка при вычислении не была достаточно существенной, чтобы на самом деле правильным ответом было 0,6.
поэтому ошибка при вычислении не была достаточно существенной, чтобы на самом деле правильным ответом было 0,6.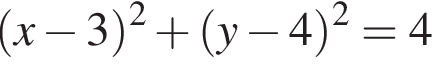 задает окружность, центр которой имеет координаты (3; 4), следовательно, длина радиуса данной окружности равна 2. График данной нам функции не имеет общих точек с окружностью. Таким образом, 1 — Г.
задает окружность, центр которой имеет координаты (3; 4), следовательно, длина радиуса данной окружности равна 2. График данной нам функции не имеет общих точек с окружностью. Таким образом, 1 — Г.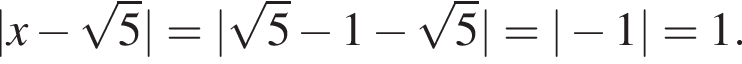

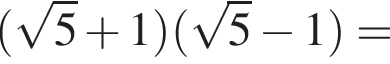
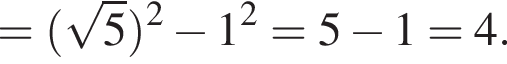


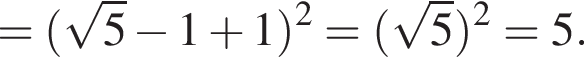
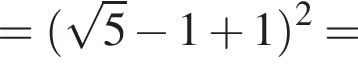
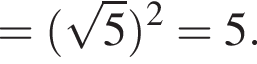
 Итак, ответ — В.
Итак, ответ — В. Углы
Углы  равны 40°. Отрезки OA и OC равны как радиусы одной окружности, поэтому треугольник AOC — равнобедренный,
равны 40°. Отрезки OA и OC равны как радиусы одной окружности, поэтому треугольник AOC — равнобедренный,  Найдем градусную меру угла
Найдем градусную меру угла 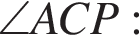
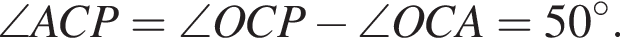
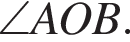 Треугольники AOB и AOC равны по трем сторонам. Найдем градусную меру угла
Треугольники AOB и AOC равны по трем сторонам. Найдем градусную меру угла 

 равна половине градусной меры дуги KC. В таком случае градусная мера дуги KC равна 80°. Ответ — Б.
равна половине градусной меры дуги KC. В таком случае градусная мера дуги KC равна 80°. Ответ — Б. Итак, 1 — Б.
Итак, 1 — Б. Таким образом, 2 — А.
Таким образом, 2 — А. Прямая BA — проекция AC на плоскость ABA1,
Прямая BA — проекция AC на плоскость ABA1,
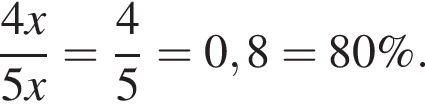
 что составляет
что составляет  откуда
откуда 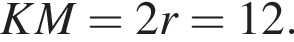 Тогда
Тогда 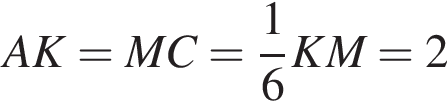 и
и 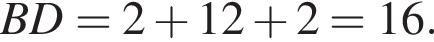 Площадь ромба равна половине произведения его диагоналей, то есть
Площадь ромба равна половине произведения его диагоналей, то есть 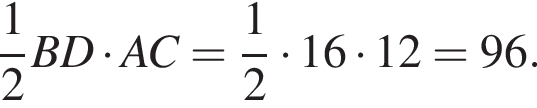
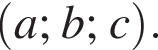 Тогда
Тогда 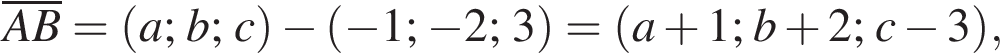

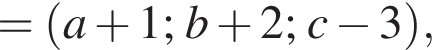
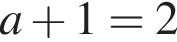 и
и 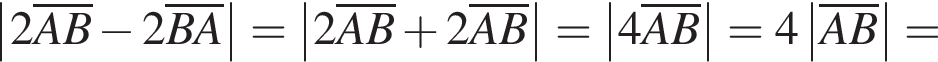
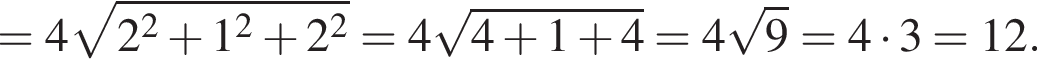
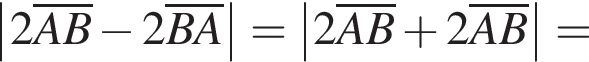
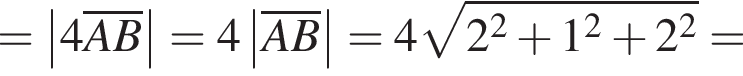
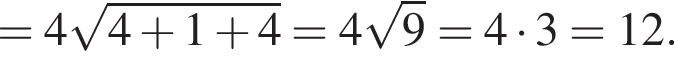

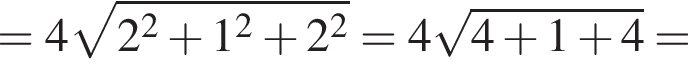
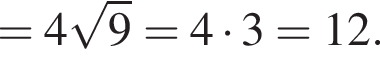
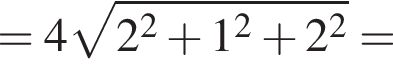
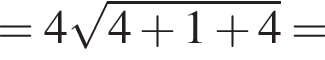
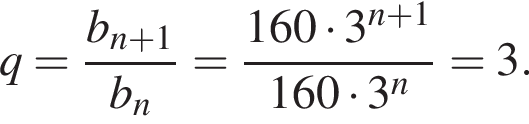
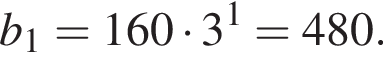 Сумма первых k членов геометрической прогрессии может быть найдена по формуле:
Сумма первых k членов геометрической прогрессии может быть найдена по формуле: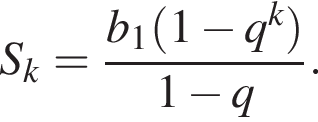
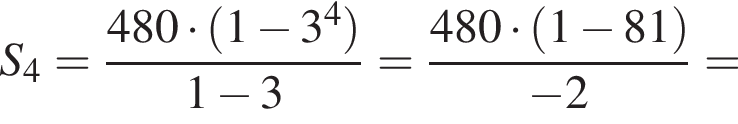
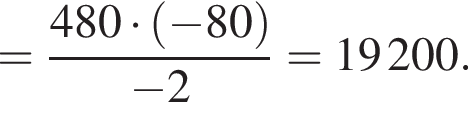
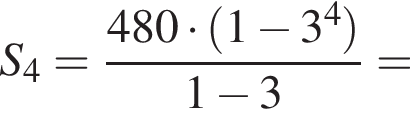
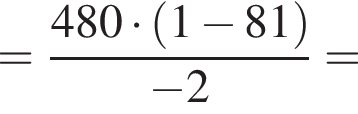
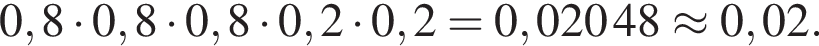

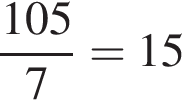 гривен в день.
гривен в день.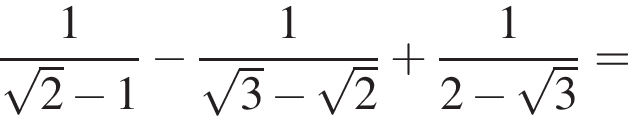
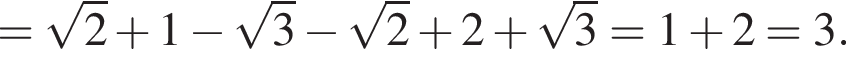
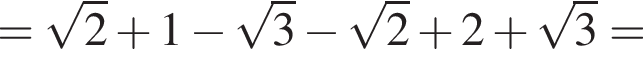
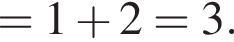

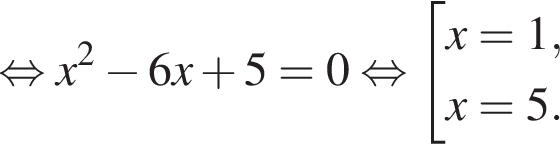
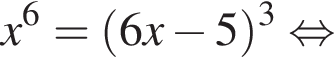
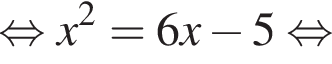
 вариантов выбора первых двух смайликов. В каждом из них есть 13 вариантов последнего смайлика, что дает окончательно
вариантов выбора первых двух смайликов. В каждом из них есть 13 вариантов последнего смайлика, что дает окончательно 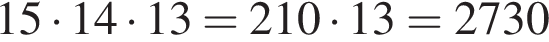 вариантов.
вариантов.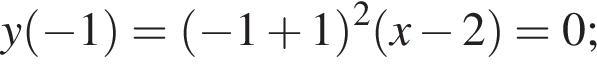
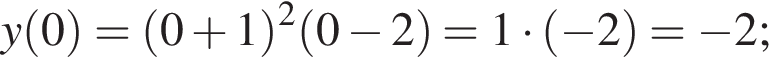
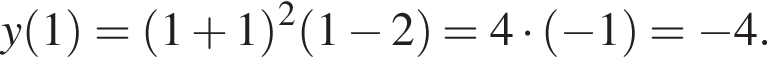
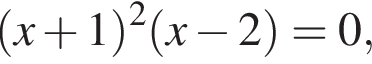 откуда
откуда 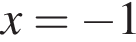 и
и 

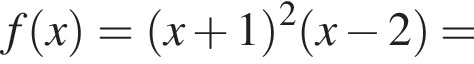
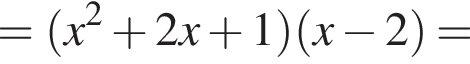
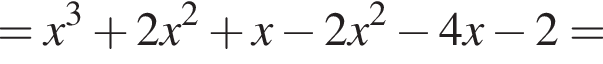
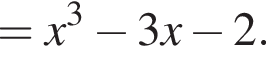
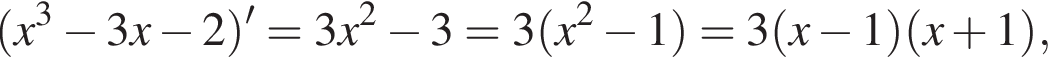
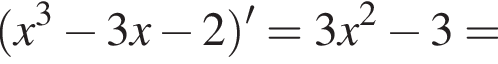
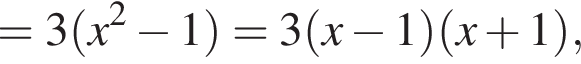
 и положительно при
и положительно при  или
или 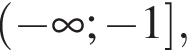 убывает на
убывает на 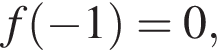
 Возьмем вторую производную
Возьмем вторую производную 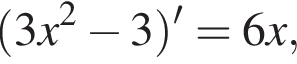 что положительно при
что положительно при  График изображен на рисунке.
График изображен на рисунке.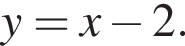 Для этого решим уравнение:
Для этого решим уравнение: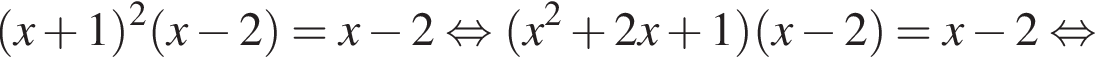
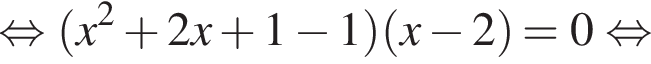
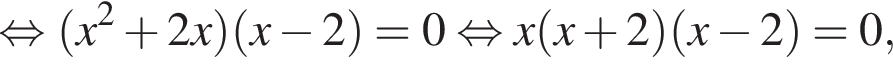
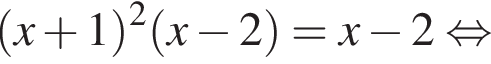
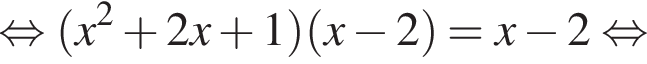
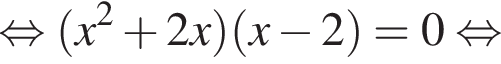
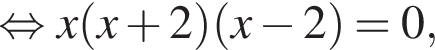
 Следовательно, прямая
Следовательно, прямая 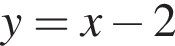 пересекает график функции при
пересекает график функции при 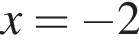 и
и 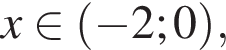 ее график лежит выше секущей. Поэтому
ее график лежит выше секущей. Поэтому 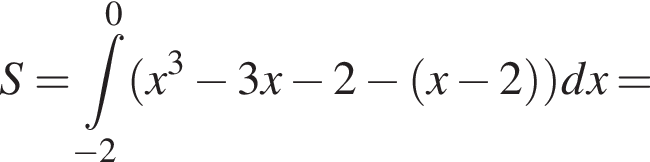
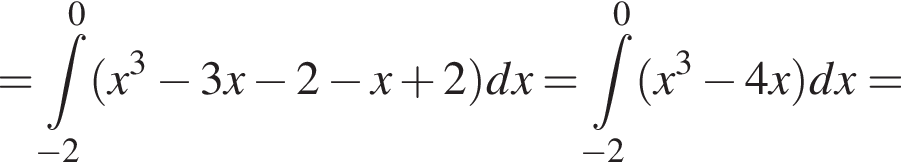
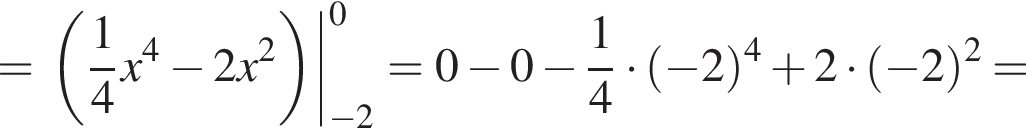
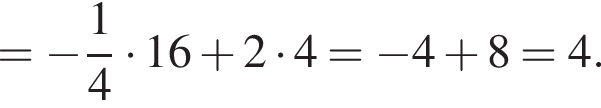
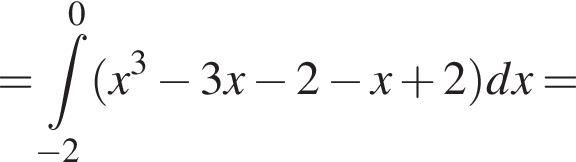
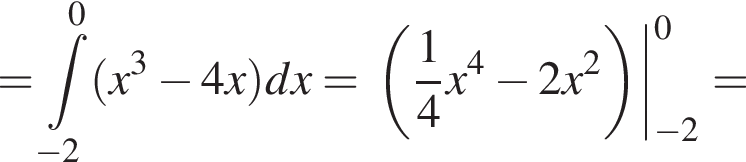
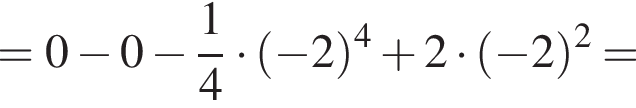
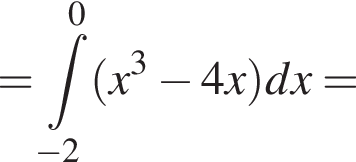
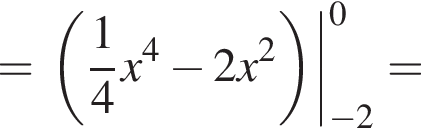
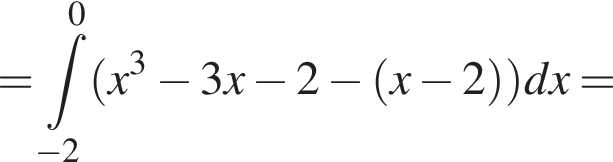
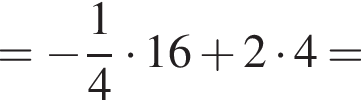

 то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.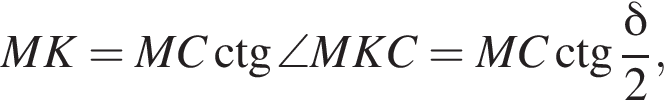
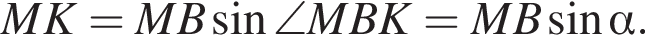
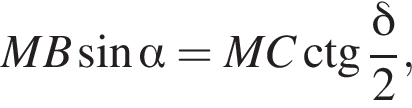 откуда
откуда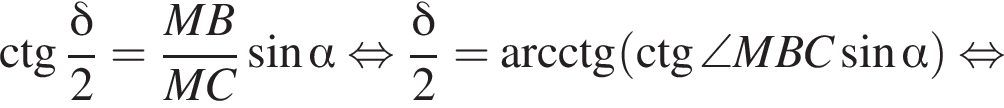
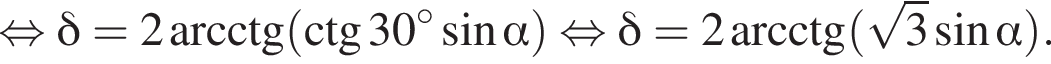

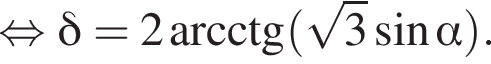
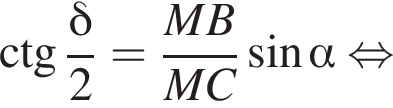
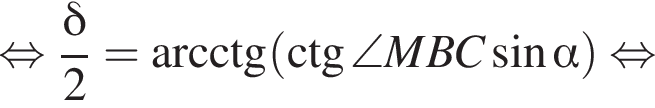

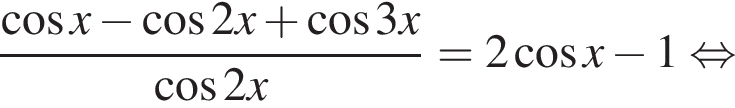
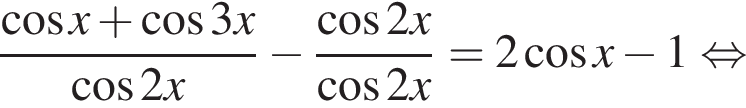
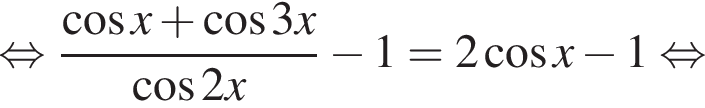
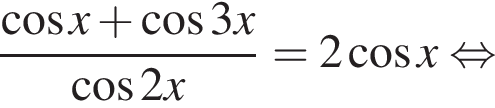
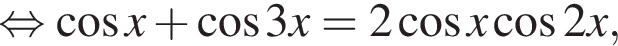

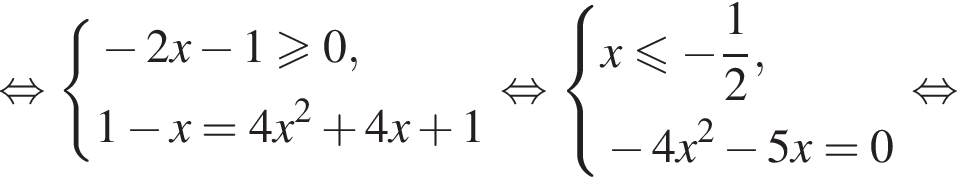
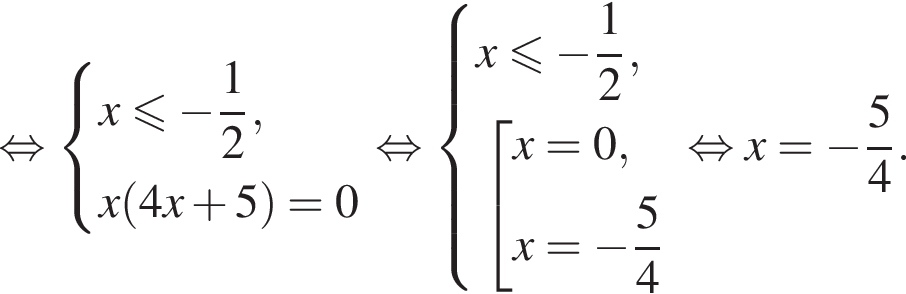
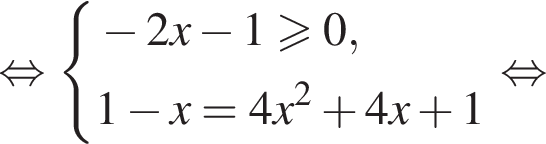
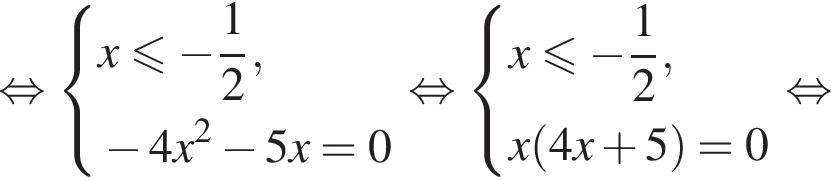
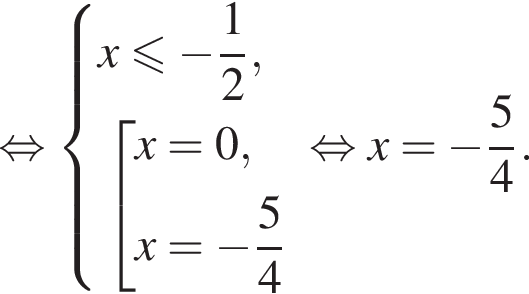
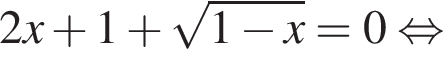
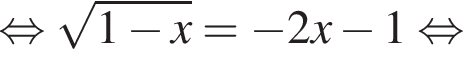
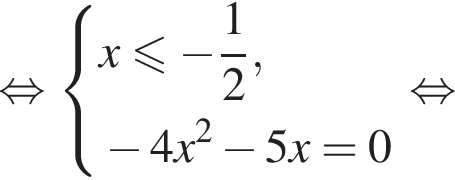
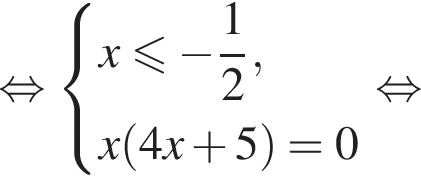
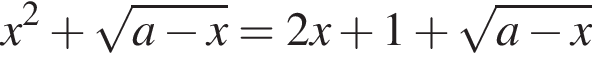 равносильно системе
равносильно системе 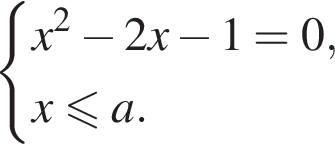 Эта система имеет единственный корень
Эта система имеет единственный корень 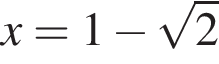 на отрезке [−1; 1] при
на отрезке [−1; 1] при 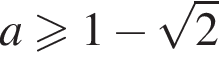 и не имеет корней на этом отрезке при других значениях a.
и не имеет корней на этом отрезке при других значениях a.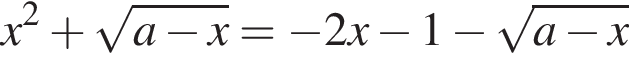 равносильно уравнению
равносильно уравнению  Оно имеет единственный корень
Оно имеет единственный корень 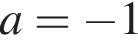 и не имеет корней на этом отрезке при других значениях a.
и не имеет корней на этом отрезке при других значениях a.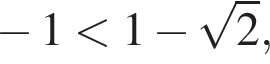 уравнение
уравнение 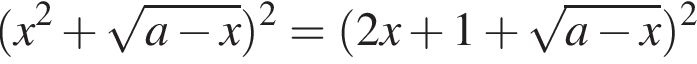 имеет единственный корень на отрезке [−1; 1] при
имеет единственный корень на отрезке [−1; 1] при 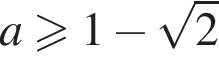 и
и