1. Тип 7 № 1157 

Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
Перетворення виразів. Прості перетворення
i
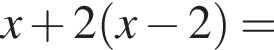
А) 3x−4
Б) 3x+4
В) 3x
Г) 3x−2
Д) 2x−2
Решение. Раскроем скобки:

Правильный ответ указан под номером 1.
Ответ: 1
1157
1
Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
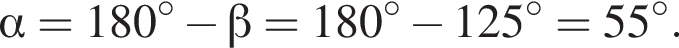
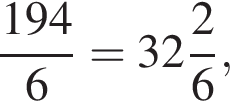 32 столов не хватит, но 33 хватит.
32 столов не хватит, но 33 хватит.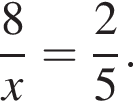
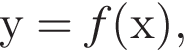 визначеної на проміжку [−3; 3]. На якому з наведених проміжків ця функція зростає?
визначеної на проміжку [−3; 3]. На якому з наведених проміжків ця функція зростає?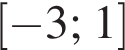 график функции идет «снизу вверх» — чем большее x из этого промежутка подставить в функцию, тем больше получится и y. Остальные промежутки не подходят — например
график функции идет «снизу вверх» — чем большее x из этого промежутка подставить в функцию, тем больше получится и y. Остальные промежутки не подходят — например  (запрещает все ответы, кроме правильного).
(запрещает все ответы, кроме правильного).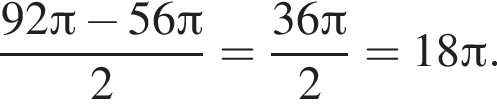

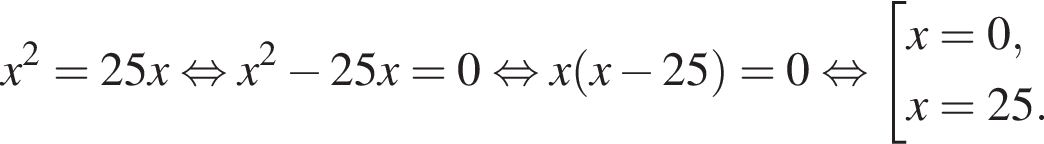
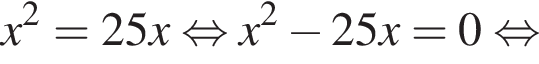
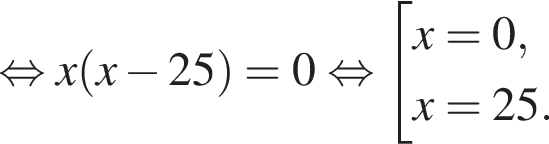
 монет, из них
монет, из них 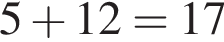 имеют номинал, меньший 50 копеек. Значит, ответ —
имеют номинал, меньший 50 копеек. Значит, ответ — 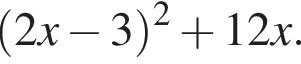
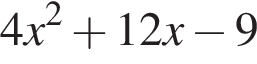
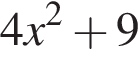
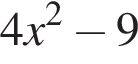
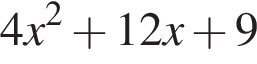
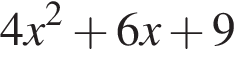
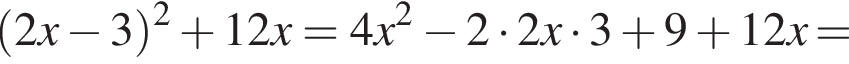
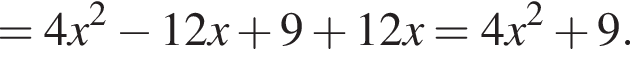
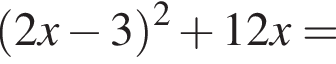
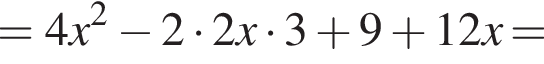
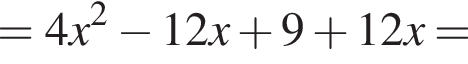
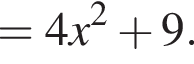

 определена только при
определена только при 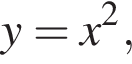 значит, годится лишь пятый график.
значит, годится лишь пятый график. 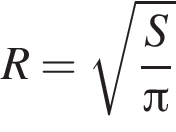
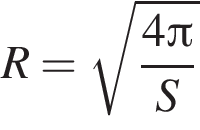

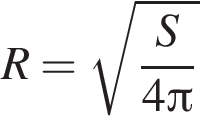
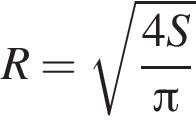
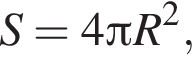 откуда
откуда 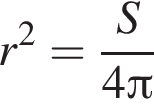 и
и 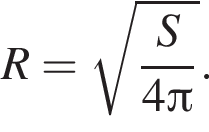
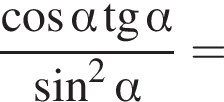
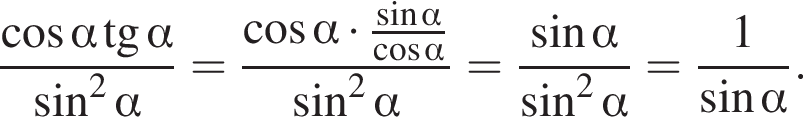
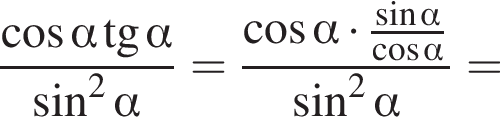
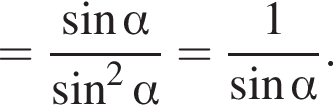
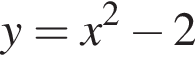
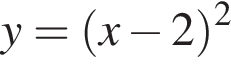
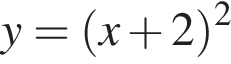
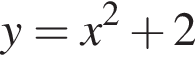
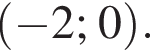 Ясно, что
Ясно, что 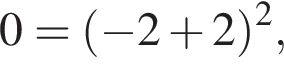 поэтому на четвертом графике эта точка лежит. Можно проверить, что в остальные уравнения эта точка не подходит.
поэтому на четвертом графике эта точка лежит. Можно проверить, что в остальные уравнения эта точка не подходит. 
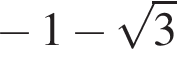
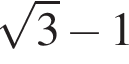
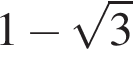
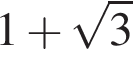
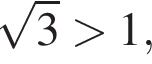 число
число 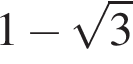 отрицательное. Поэтому
отрицательное. Поэтому 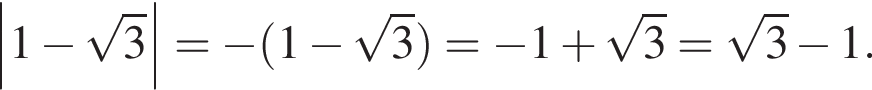
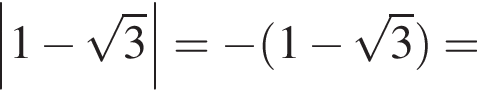
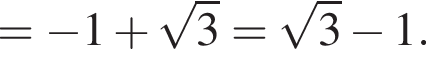
 то есть
то есть 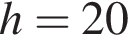 см
см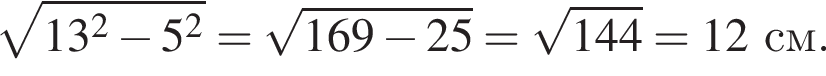

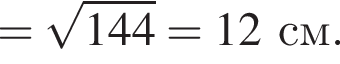
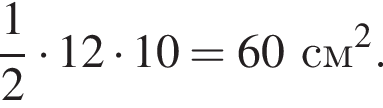

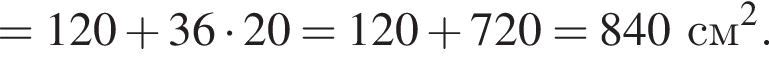

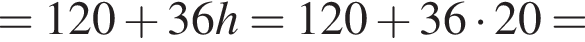
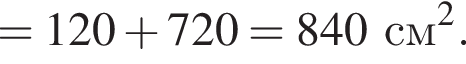





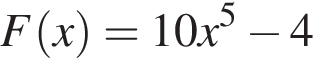 є первісною функції f(х). Укажіть функцію G(х), яка також є первісною функції f(х).
є первісною функції f(х). Укажіть функцію G(х), яка також є первісною функції f(х).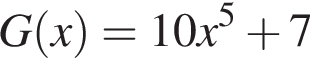
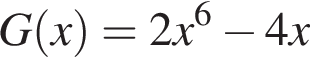


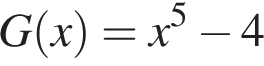
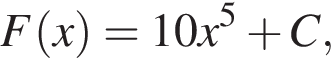 где С — произвольное число. Тогда:
где С — произвольное число. Тогда: 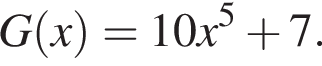
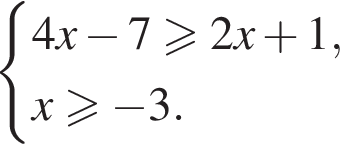
 то есть
то есть  м, а также оно составляет
м, а также оно составляет  м. Следовательно,
м. Следовательно,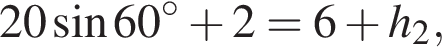
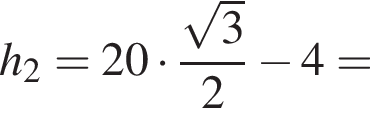
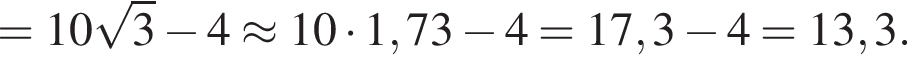
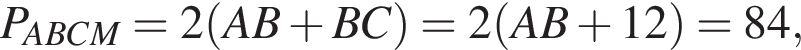
 Прямые AB и CM параллельны по условию, прямые BC и AM параллельны по свойству трапеции. Таким образом, ABCM — параллелограмм. Следовательно, 1 — Б.
Прямые AB и CM параллельны по условию, прямые BC и AM параллельны по свойству трапеции. Таким образом, ABCM — параллелограмм. Следовательно, 1 — Б.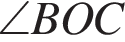 и
и 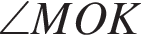 равны как вертикальные углы. Углы
равны как вертикальные углы. Углы  и
и 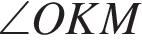 равны как внутренние разносторонние. Тогда:
равны как внутренние разносторонние. Тогда: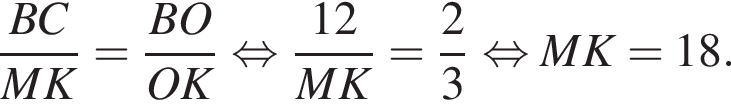

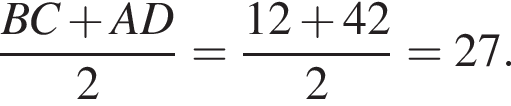

 В прямоугольном треугольнике AOB по теореме Пифагора:
В прямоугольном треугольнике AOB по теореме Пифагора: 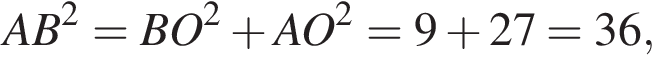
 Значит, 2 — А.
Значит, 2 — А. где
где  Имеем:
Имеем: 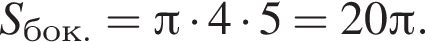 Итак, 3 — Г.
Итак, 3 — Г.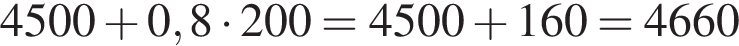
 гривен. Значит, он заплатит
гривен. Значит, он заплатит 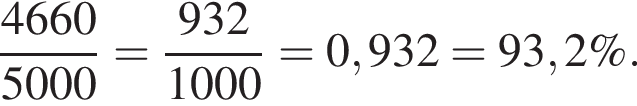
 см
см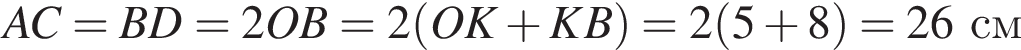

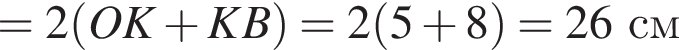
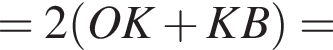
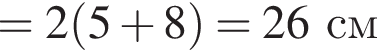
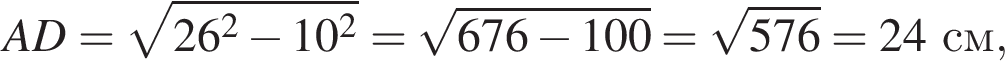
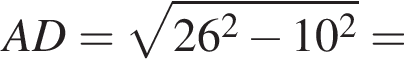

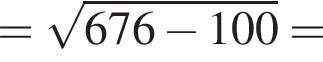
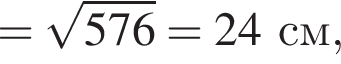

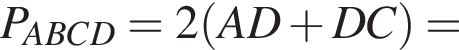
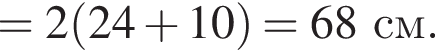

 тогда
тогда 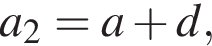
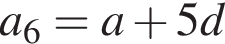 и по условию
и по условию 
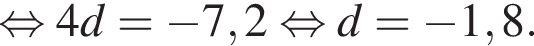
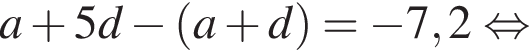
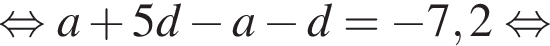
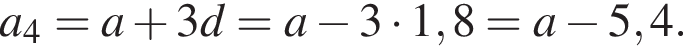
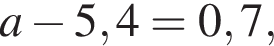 откуда
откуда 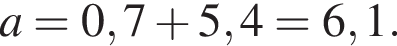

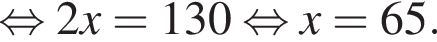
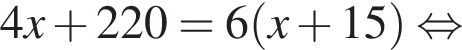
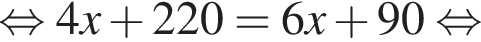
 тетрадей Алексей заплатил
тетрадей Алексей заплатил 
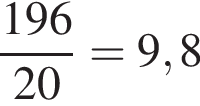 гривны.
гривны.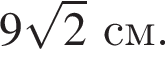 Визначте об'єм цiєї пiрамiдi (у см3).
Визначте об'єм цiєї пiрамiдi (у см3).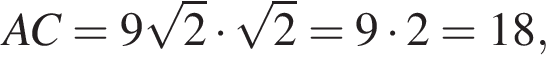
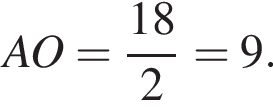 В прямоугольном треугольнике SOA по теореме Пифагора получаем
В прямоугольном треугольнике SOA по теореме Пифагора получаем 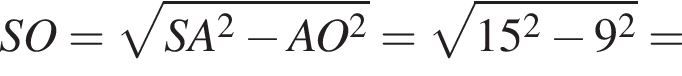
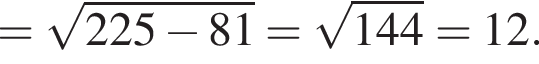

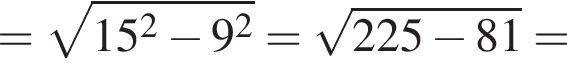
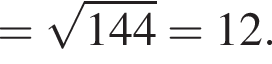
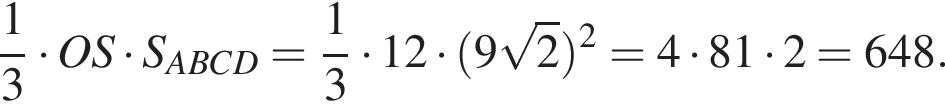
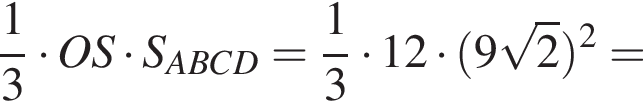
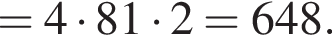
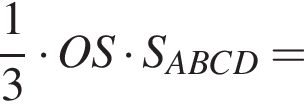
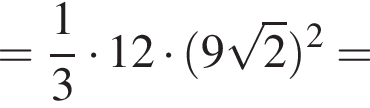
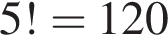 способов. Окончательный ответ
способов. Окончательный ответ  способов.
способов.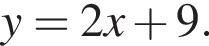
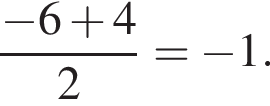 Итак, абсцисса B это −1, тогда ее ордината
Итак, абсцисса B это −1, тогда ее ордината 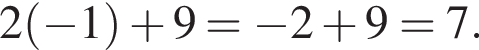
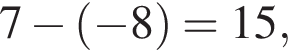 а длина основания AC равна
а длина основания AC равна 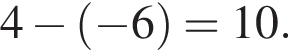 Поэтому его площадь
Поэтому его площадь 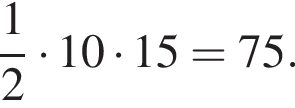
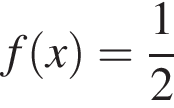 та
та 
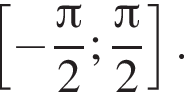
 на інтервалі (−∞; +∞).
на інтервалі (−∞; +∞). также построена на рисунке. Общей точкой будет
также построена на рисунке. Общей точкой будет 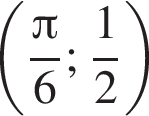 и только она — при
и только она — при 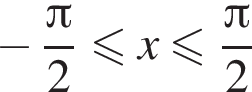 функция
функция 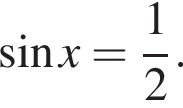 Это стандартное тригонометрическое уравнение с ответом
Это стандартное тригонометрическое уравнение с ответом 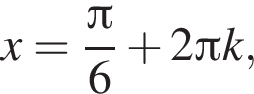
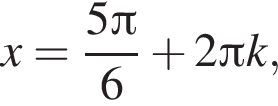
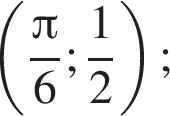
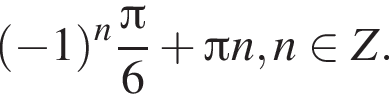
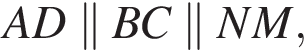 поэтому AD и MN лежат в одной плоскости. Очевидно это и есть плоскость
поэтому AD и MN лежат в одной плоскости. Очевидно это и есть плоскость 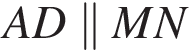 и
и 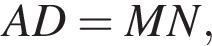 кроме того
кроме того  и
и 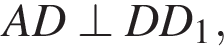 значит
значит  а потому
а потому  Найдем его площадь. Пусть
Найдем его площадь. Пусть 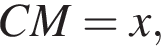 тогда
тогда  Поскольку проекция CB1 на плоскость CC1D1D это прямая CC1, то
Поскольку проекция CB1 на плоскость CC1D1D это прямая CC1, то 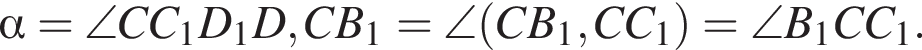
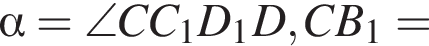
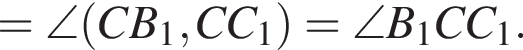
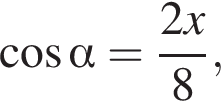 откуда
откуда 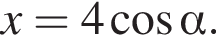 Кроме того,
Кроме того, 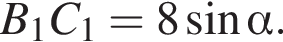 Наконец,
Наконец, 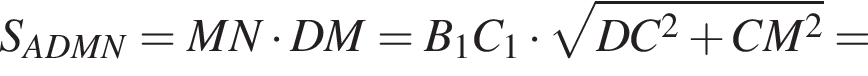
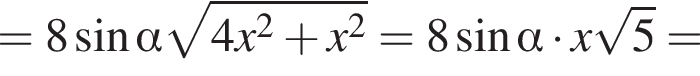

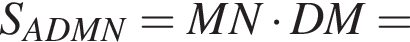
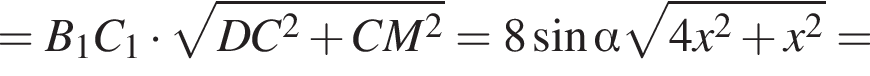
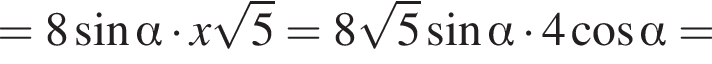
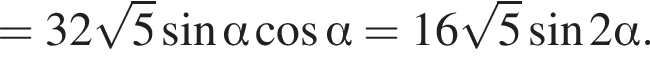

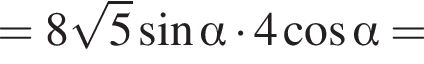
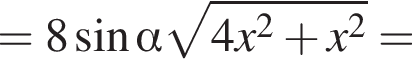
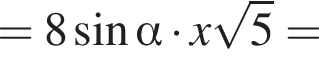



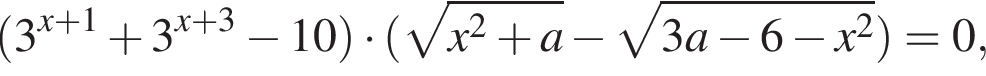
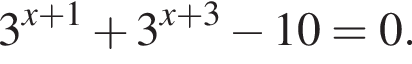
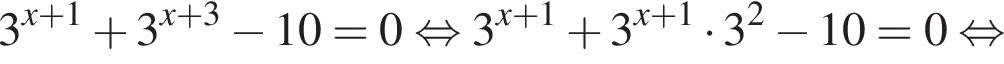

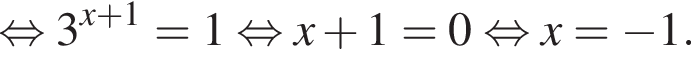
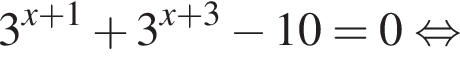
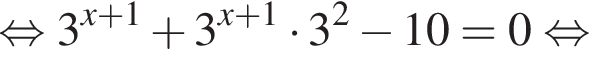
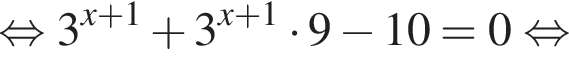
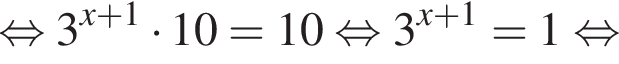
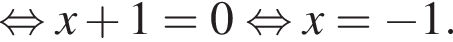
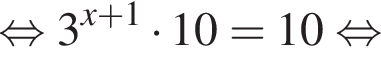
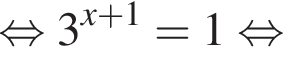

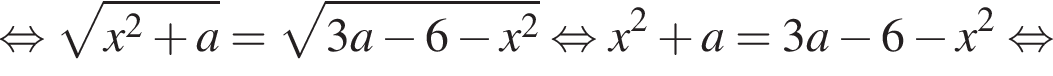


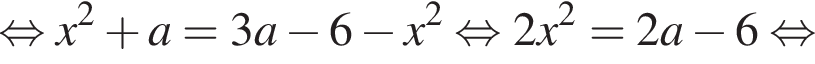

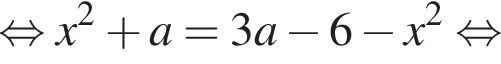
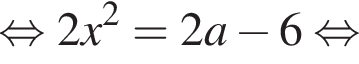
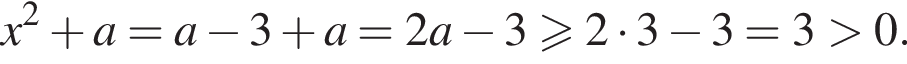
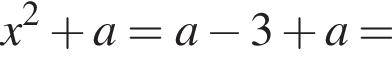
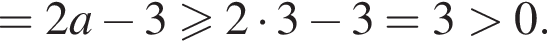
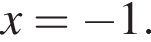 Для этого должны быть неотрицательны оба подкоренных выражения, то есть
Для этого должны быть неотрицательны оба подкоренных выражения, то есть 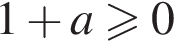 и
и  откуда
откуда 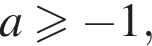 это более слабое условие).
это более слабое условие).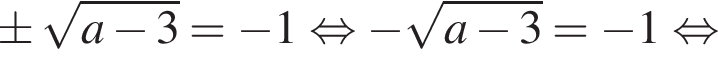
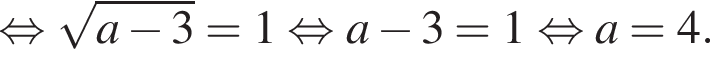
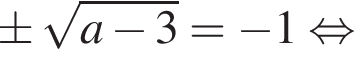
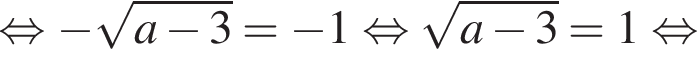
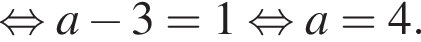
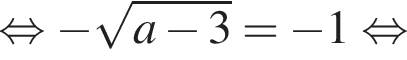
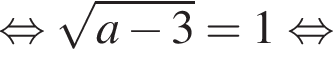
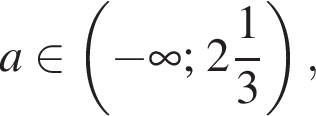 то рівняння коренів не має;
то рівняння коренів не має;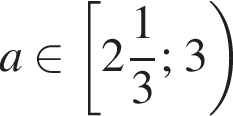 , то
, то 
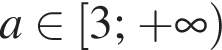 , то
, то 