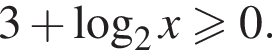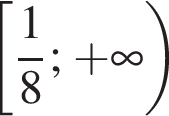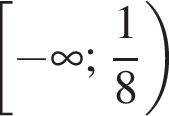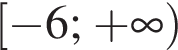Розташуйте у порядку спадання числа ![]()
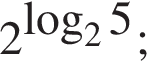
![]()
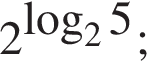
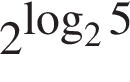
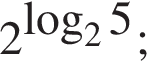
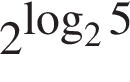
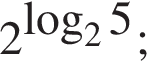
Розташуйте у порядку спадання числа ![]()
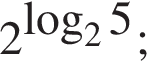
![]()
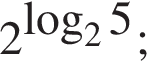
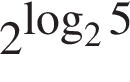
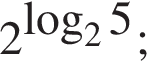
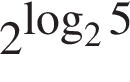
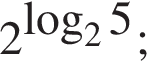
Банк сплачує своїм вкладникам 8% річних. Визначте, скільки грошей треба покласти на рахунок, шоб через рік отримати 60 грн. прибутку.
З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?
Розв'яжіть нерівність 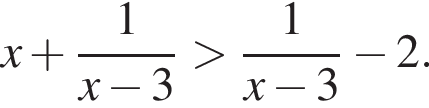
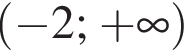


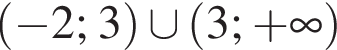
Будівельна компанія закупила для нового будинку металопластикові вікна та двері у відношенні 4 : 1. Укажіть число, яким може виражатися загальна кількість вікон та дверей в цьому будинку.
Обчисліть 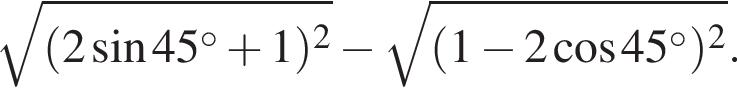
Розв яжіть ршняння 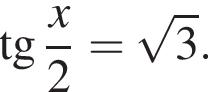
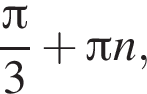
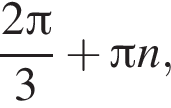
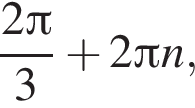
Обчисліть 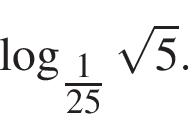
Розв'яжіть нерівність 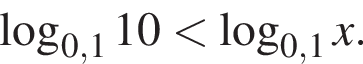
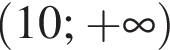
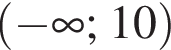
Розв'яжіть рівняння 
Укажіть, скільки дійсних коренів має рівняння 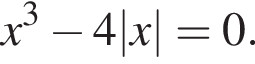
На перегоні, довжина якого дорівнює 240 км, поїзд рухався зі швидкістю на 10 км/год менше, ніж мала бути за розкладом, і запізнився на 48 хв. З якою швидкістю мав рухатися поїзд за розкладом? Відповідь в км/год.
Знайдіть натуральне, одноцифрове число N, якшо відомо, шо сума 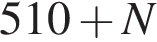 ділиться на 9 без остачі.
ділиться на 9 без остачі.
Визначте кількість усіх дробів із знаменником 28, які більші за ![]() але менші від
але менші від ![]()
Під час закладання нового парку 25% його плоші відвели під посадку кленів, 50% плоші, шо залишилася, — під посадку дубів, а решту плоші — під газони. Вкажіть, на якій із діаграм правильно показано розподіл посадок.
Розв'яжіть нерівність 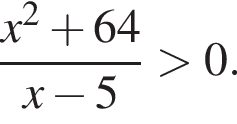



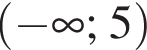
Якшо 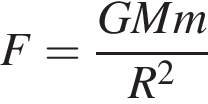 i
i ![]() то R?
то R?
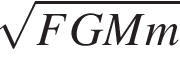
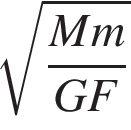
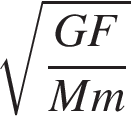
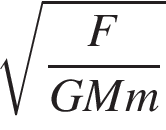
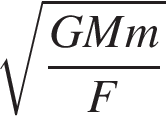
Укажіть правильну нерівність, якшо 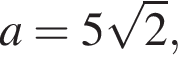
![]()

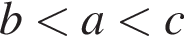
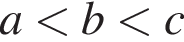
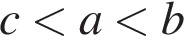
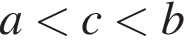
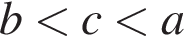
Розв'яжіть рівняннл 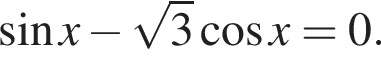
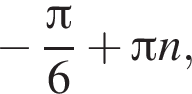
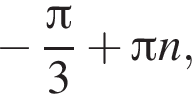
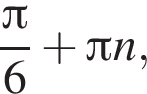
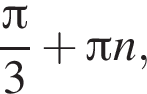
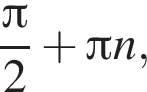
Обчисліть 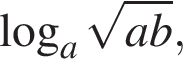 якшо
якшо 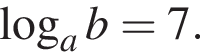
Укажіть, скільки можна скласти різних правильних дробів, чисельниками і знаменниками яких є числа 2, 3, 4, 5, б, 7, 8, 9.
Розв'яжiть нерівність 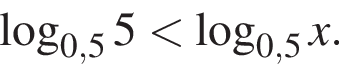

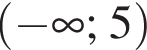
Укажіть корінь рівняння 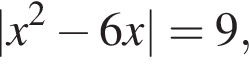 який належить проміжку (−2; 1].
який належить проміжку (−2; 1].
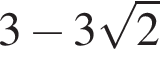
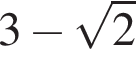
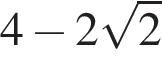
Розв:яжіть рівняння: 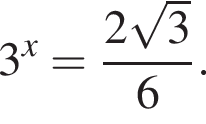
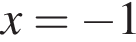
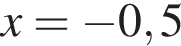

Знайдіть значення вираз 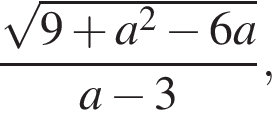 якщо
якщо 
Спростіть вираз 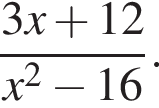
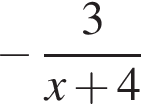
Обчисліть 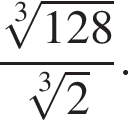
Яка з поданих нижче послідовностей є арифметичною прогресією? −9; −2; 0; 1
У Оксани є певна кількість горіхів. Коли вона розклала їх у купки по 5 горіхів, то два горіхи залишилися, а коли розклала їх по 3, то зайвих горіхів не виявилося. Яка кількість горіхів із запропонованих варіантів МОГЛА БУТИ в Оксани?
Розв’яжіть нерівність 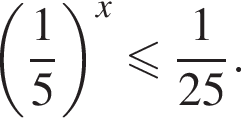
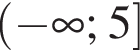
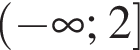


За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми переказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30 000 грн.
Якщо 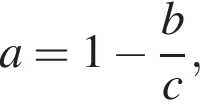 то b?
то b?
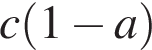
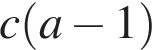
Укажіть правильну нерівність.
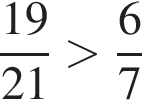
У туриста є 10 однакових за розмірами консервних банок, серед яких 4 банки — з тушкованим м’ясом, 6 банок — з рибою. Під час зливи етикетки відклеїлися. Турист навмання взяв одну банку. Яка ймовірність того, ідо вона буде з рибою?
Розв’яжіть рівняння 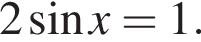
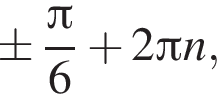
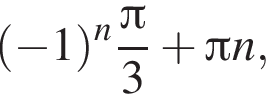
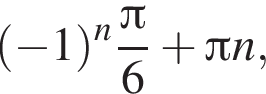
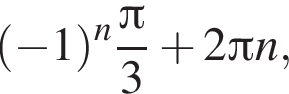
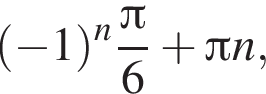
До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні дві команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон?
Свинцеву кулю радіуса 5 см переплавили в кульки однакового розміру, радіус кожної з яких — 1 см. Скільки таких кульок одержали? Втратами свинцю під час переплавлення знехтуйте.
Розв'яжіть нерівність 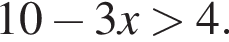
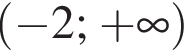

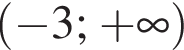
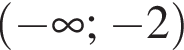
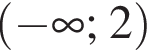
Обчисліть 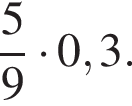
За видачу свідоцтва про право на спадщину стягується державне мито в розмірі 0,5% від вартості майна, що успадковується. Скільки державного мита повинен сплатити спадкоємець, якщо вартість майна, що успадковується, становить 32 000 грн?
Спростіть вираз 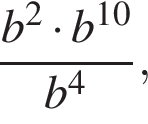 де
де ![]()
Якому з наведених проміжків належить корінь рівняння 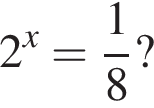
Обчисліть 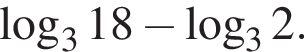
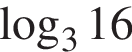
Спростіть вираз 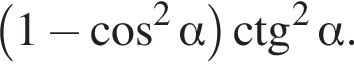
Пасічник зберігає мед в однакових закритих металевих бідонах. Їх у нього дванадцять: у трьох бідонах міститься квітковий мед, у чотирьох — мед із липи, у п’яти — мед із гречки. Знайдіть імовірність того, що перший навмання відкритий бідон буде містити квітковий мед.
Якому з наведених проміжків належить число ![]()
Студенти однісі з груп під час сесії повинні скласти п'ять іспитів. Заступнику декана потрібно призначити складання цих іспитів на п'ять визначених дат. Скільки всього існує різних варіантів розкладу іспитів для цієї групи?
Цеглина має форму прямокутного паралелепіпеда 3 вимірами 25 см, 12 см, 6,5 см. Знайдіть масу m цеглини. Для знаходження маси цеглини скористайтеся формулою  де V — об'єм,
де V — об'єм,  г/см3
г/см3
Обчисліть 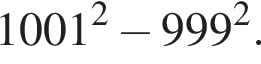
Перед Новим роком у магазині побутової техніки на всі товари було знижено ціни на 15%. Скільки коштуватиме після знижки телевізор вартістю 1800 грн?
Обчисліть 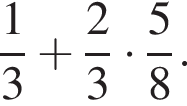
Cпростіть вираз 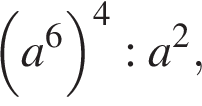 де
де ![]()
Обчисліть 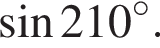
Розв яжіть систему
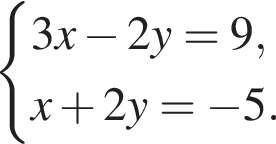
Для одержаного розв'язку (x0; у0) обчисліть суму 
Серед чисел 
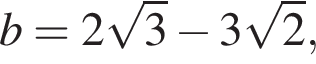
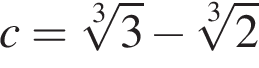 укажіть усі додатні.
укажіть усі додатні.
Якому з наведених проміжків належить корінь рівняння 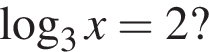
На полиці знаходяться 18 однакових скляних банок із джемом. Серед них 6 банок з абрикосовим джемом, 12 — з яблучним. За кольором джеми не відрізняються один від одного. Господиня навмання взяла одну банку. Яка ймовірність того, що вона буде з абрикосовим джемом?
Кодовий замок на дверях має десять кнопок, на яких нанесено десять різних цифр (див. рисунок). Щоб відчинити двері, потрібно одночасно натиснути дві кнопки, цифри на яких складають код замка. Скільки всього існує різних варіантів коду замка? Уважайте, що коди, утворені перестановкою цифр (наприклад, 1−2 і 2−1), є однаковими.
У саду в окремі ящики зібрали груші та яблука. Кількість ящиків з яблуками відноситься до кількості ящиків з грушами,
Поле, площа якого дорівнюе 60 га, засіяли горохом і соєю. Горохом засіяли ![]() площі поля. Скільки всього гектарів поля засіяли соєю?
площі поля. Скільки всього гектарів поля засіяли соєю?
Якому з наведених проміжків належить корінь рівняння 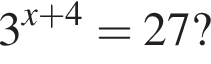
Яке з наведених чисел е раціональним числом?
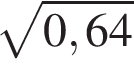
Знайдіть найбільший від’ємний член арифметичної прогресії 2,9; 2,2; 1,5; ...
Упродовж чверті учень отримав 12 оцінок з алгебри. Інформацію про отримані оцінки та їхню кількість відображено в таблиці.
| Оцінка | 5 | 6 | 7 | 8 | 10 |
| Кількість оцінок | 2 | 1 | 3 | 5 | 1 |
Знайдіть середнє арифметичне всіх оцінок, отриманих учнем упродовж чверті.
Облисліть 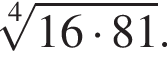
Розташуйте в порядку зростання числа 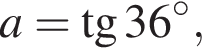
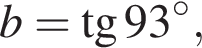
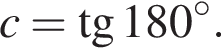
Подайте вираз ![]() у вигляді степеня з основою a.
у вигляді степеня з основою a.
На полиці розміщено 16 книг, з яких 6 книг — історичні романи, а решта - детективи. Знайдіть імовірність того, що перша книга, навмання взята з полиці, буде детективом.
Розв’яжіть нерівність 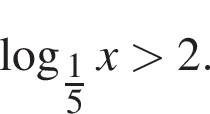
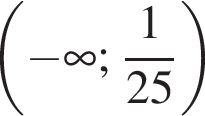
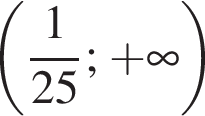
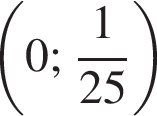
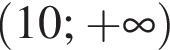
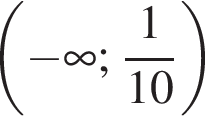
У кіоску є 10 видів вітальних листівок з Новим роком. Скільки всього можна утворити різних наборів листівок, кожен із яких складається з трьох листівок різних видів?
Молоко містить 3% білків. Скільки всього білків (у г) міститься в 600 г молока?
Задано геометричну прогресію (bn), для якої другий член  і знаменник
і знаменник 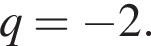 Знайдіть b1.
Знайдіть b1.
Відомо, що ![]() Серед наведених нерівностей укажіть правильну нерівність.
Серед наведених нерівностей укажіть правильну нерівність.

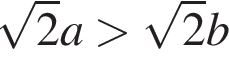

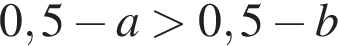
Обчисліть 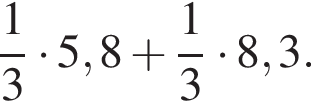
Cпростіть вираз 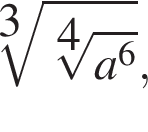 якщо
якщо ![]()
Лучник здійснив 11 пострілів по мішені і набрав відповідно 6, 5, 7, 9, 6, 9,10, 8, 7, 9, 10 очок. Знайдіть моду цього ряду даних.
Обчисліть 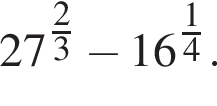
Якщо 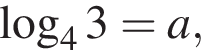 то
то 
Розв'яжіть нерівність 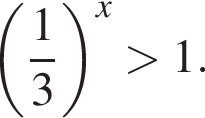
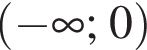
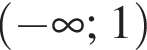



У лотереї 10 виграшних білетів і 290 білетів без виграшу. Яка ймовірність того, що перший придбаний білет цієї лотереї буде виграшним?
У магазині придбали 6 однакових зошитів і кілька ручок по 3 грн за кожну з них. Яке з наведених чисел може виражати загальну вартість покупки (у грн)?
Знайдіть найменший додатний корінь рівняння 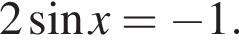
Скільки всього різних п'ятицифрових чисел можна утворити з цифр 0, 1, 3, 5, 7 (у числах цифри не повинні повторюватися)?
Розв'яжіть рівняння ![]()

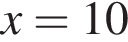



Спростіть вираз 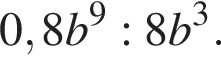
Обчисліть 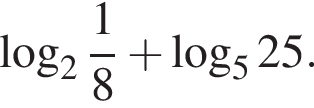
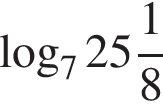
На рисунку зображено куб ABCDA1B1C1D1. Укажіть серед поданих нижче пряму, що утворюе з CD1 пару мимобіжних прямих.
Журнал коштував 25 грн. Через два місяці цей самий журнал став коштувати 21 грн. На скільки відсотків знизилася ціна журналу?
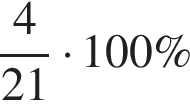
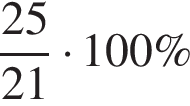
На одиничному колі зображено точку
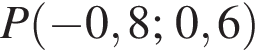 і кут α (див. рисунок). Визначте
і кут α (див. рисунок). Визначте ![]()
Спростіть вираз  якщо
якщо ![]()
Визначте знаменник геометричної прогресії (bn), якщо 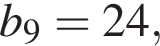
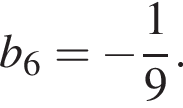
Розв'яжіть нерівність 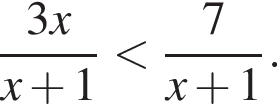
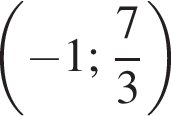
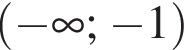
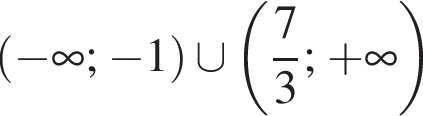
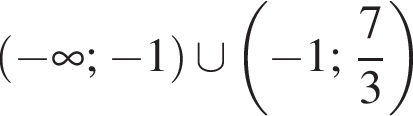
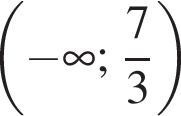
Якому з наведених нижче проміжків належить корінь рівняння 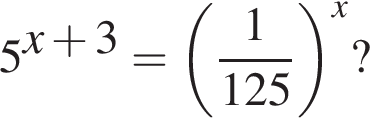
Розв'яжіть нерівність 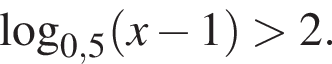

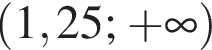
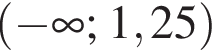
Яку 3 наведених цифр потрібно поставити замість зірочки в записі числа ![]() щоб отримане число ділилося націло на 3?
щоб отримане число ділилося націло на 3?
Обчисліть 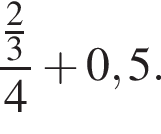
Розв'яжіть нерівність 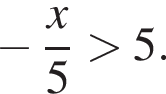
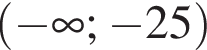
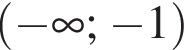
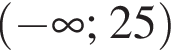
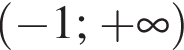
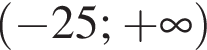
Яке з наведених чисеп е ірраціональним числом?
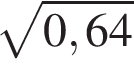
Обчисліть 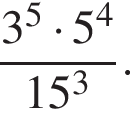
Укажіть суму коренів рівняння 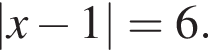
Якщо 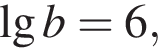 то
то 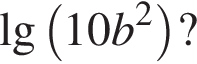
Якому з наведених проміжків належить корінь рівняння 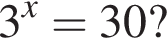
В арифметичній прогресії (an) 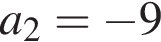 та
та 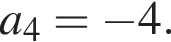 Визначте різницю цієї прогресії.
Визначте різницю цієї прогресії.
Обчисліть 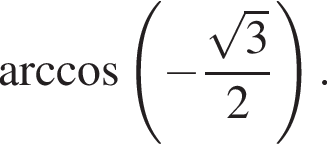
На діаграмі відображено кількість відвідувачів Музею Води протягом одного робочого тижня (з вівторка до неділі). У який день тижня кількість відвідувачів була вдвічі більшою, ніж у попередній день?
Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 5000 грн, розподіливши гроші таким чином: перший отримав четверту частину зароблених грошей, а другий — решту. Скільки гривень отримав за цю роботу другий фахівець?
Запишіть числа ![]() 1,
1, ![]() в порядку зростання.
в порядку зростання.
У залі кінотеатру 18 рядів. У першому ряду знаходяться 7 місць, а в кожному наступному ряду на 2 місця більше, ніж у попередньому. Скільки всього місць у цьому залі?
Якому проміжку належить значення виразу 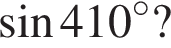
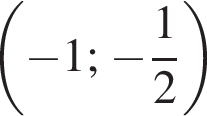
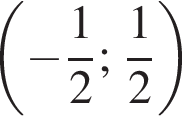
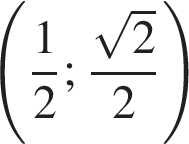
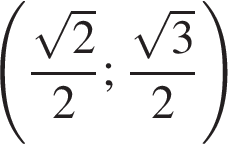
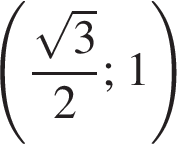
3 міст A і B, відстань між якими по шосе становить 340 км, одночасно назустріч один одному виїхали автобус і маршрутне таксі зі сталими швидкостями 65 км/год әод і 80 км/год відповідно. Автобус і маршрутне таксі рухаються без зупинок і ще не зустрілися. За якою формулою можна обчислити відстань S (у км) між автобусом і маршрутним таксі по шосе через t годин після початку руху?
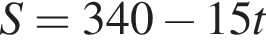
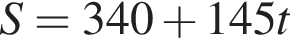
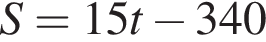

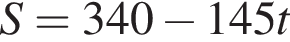
Розв'яжіть нерівність 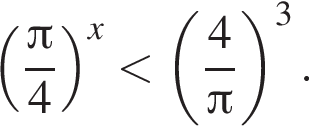
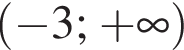

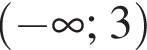
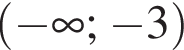
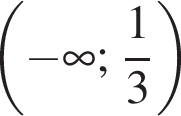
Укажіть множину всіх значень a, при яких виконуеться рівність 

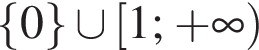
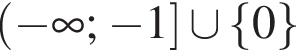
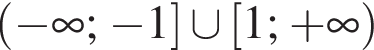
Функція f(x) має в точці x0 похідну 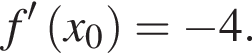 Визначте значення похідної функції
Визначте значення похідної функції 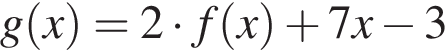 в точці x0.
в точці x0.
На рисунку показано жирними точками найвищу і найнижчу температури повітря кожного дня тижня з понеділка до п'ятниці в деякому місті України. По горизонталі відмічено дні тижня, а по вертикалі — температуру повітря в градусах Цельсія. У який день різниця між найвищою та найнижчою температурами повітря була найбільшою?
Протягом тижня два кур’ери разом доставили 210 пакепв. Ктькосл пакенв, доставлених першим i другим кур’єрами за цей перюд, вщносяться як 3 : 7. Сюльки пакепв доставив другий кур’єр?
У магазині побутової техніки діє акція: на першу велику покупку (вартість перевищує 1000 грн) надається знижка ЗО грн, на кожну наступну велику покупку попередня знижка збільшується на 25 грн. На яку за рахунком велику покупку отримає в цьому магазині покупець знижку 180 грн?
Укажіть проміжок, якому належить значення виразу 
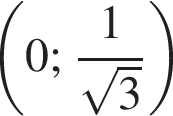
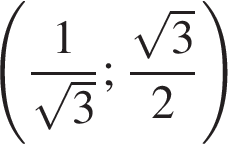
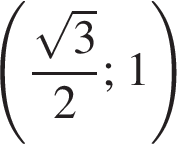
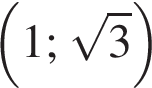
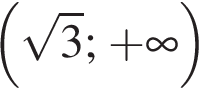
Розв'яжіть нерівність 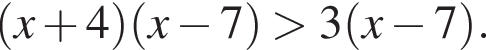

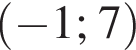
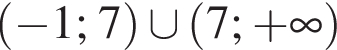
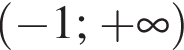
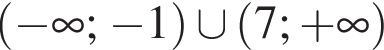
Запишіть числа 215, 410, 105 у порядку зростання.
Визначте m із співвідношення 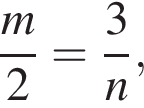 де
де ![]()
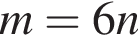
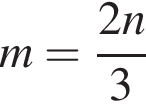
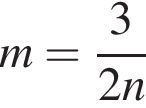
Укажіть вираз, тотожно рівний виразу 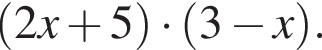
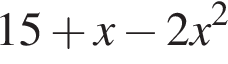
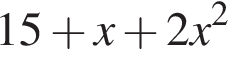
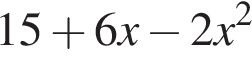
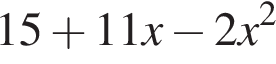
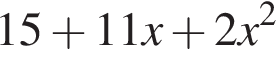
Обчисливши 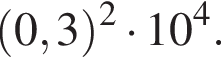
Укажіть розмах ряду даних 3, 5, 5, 13, 18, 15, 12.
Обчисліть 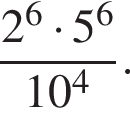
Розв'яжіть рівняння 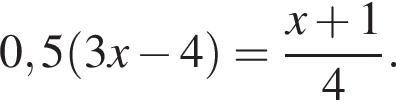
В арифметичній прогресії (an) задано ![]() та
та 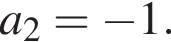 Укажіть формулу для знаходження
Укажіть формулу для знаходження

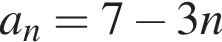
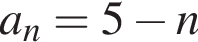
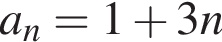
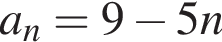
Верстат з автоматичним управлінням працює зі сталою продуктивністю і виготовляє 40 деталей за t год  Укажіть вираз для визначення кількості деталей, які виготовив верстат за 5 год.
Укажіть вираз для визначення кількості деталей, які виготовив верстат за 5 год.
Розв'яжіть систему рівнянь
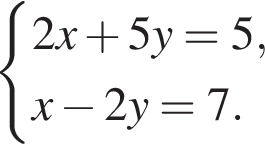
Для одержаного розв'язку (x0; y0) системи знайдіть суму 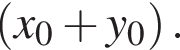
Скільки всього розв'язків мае система рівнянь
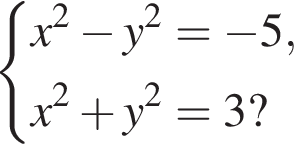
З певного аеропорту за розкладом авіарейси виконуються через кожні 10 хв. Перший літак за розкладом відлітає о шостій годині ранку. Укажіть час відльоту за розкладом тридцятого за рахунком літака.
Обчисліть 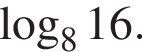
Яке з наведених рівнянь має безліч коренів?
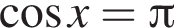
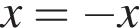
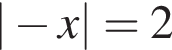

Укажіть проміжок, якому належить корінь рівняння 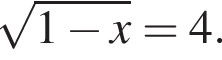
Спростіть вираз 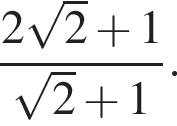
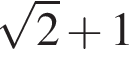
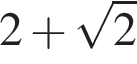
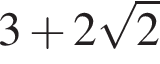
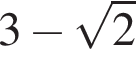
Розв'яжіть нерівність 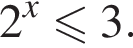
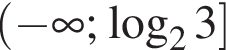
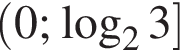
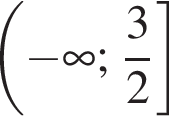
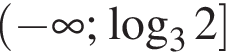
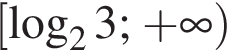
Обчисливши 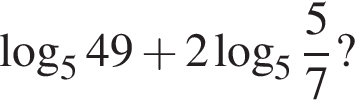
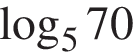
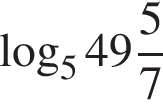
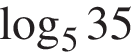
Укажіть нерівність, що виконується для 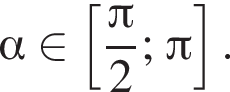
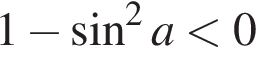
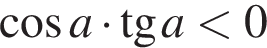
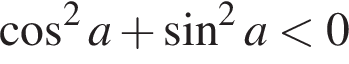
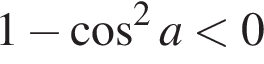

Діаграма, зображена на рисунку, містить інформацію про кількість електроенергії (у кВт — год), спожитої певною сім'єю в кожному місяці 2012 року. Користуючись діаграмою, установіть, які з наведених тверджень є правильними.
I. У грудні порівняно з липнем спожито електроенергії більше, ніж у 2 рази.
II. ЗЗа всі літні місяці спожито електроенергії на 150 кВт — год менше, ніж за всі весняні місяці.
III. Середньомісячне споживання електроенергії за рік є більшим за 120 кВт — год.
Остача від ділення натурального числа к на 5 дорівнює 2. Укажіть остачу від ділення на 5 числа 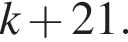
У геометричній прогресії (bn) задано  i
i 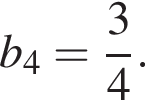 Знайдіть знаменник цієї прoгpeciї.
Знайдіть знаменник цієї прoгpeciї.
Розв'яжіть рівняння 
Розв'яжіть нерівність 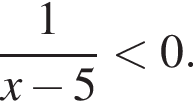
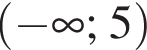
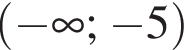

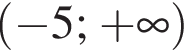

Якщо  і
і 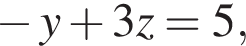 то x?
то x?
Обчисливши ![]()
Знайдіть значення виразу 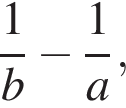 якщо
якщо
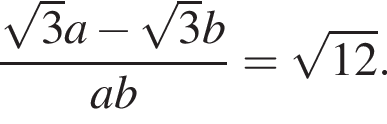
Спростіть вираз 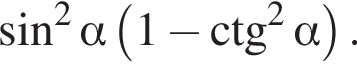


Розв'яжіть нерівність 
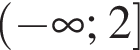


Розташуйте в порядку зростання числа ![]() 0,1; 0,11.
0,1; 0,11.
Діаграма, зображена на рисунку, містить інформацію про кількість проданих одиниць техніки в супермаркеті електроніки протягом одного кварталу.
Використовуючи дані діаграми, доберіть таке закінчення речення, щоб утворилося правильне твердження: «Більше ніж цифрових фотоапаратів, але менше ніж мобільних телефонів, у цьому супермаркеті продано...».
Розв'яжіть рівняння 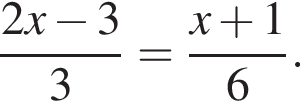
Якщо 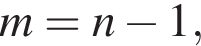 то
то 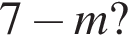
Укажіть рівняння, коренем якого є число 2.
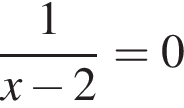
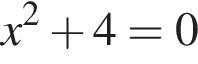
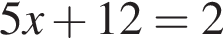
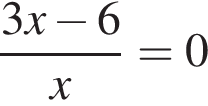
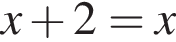
Обчисліть 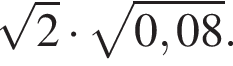
Студент на першому курсі повинен вибрати одну з трьох іноземних мов, яку вивчатиме, та одну з п'яти спортивних секцій, що відвідуватиме. Скільки всього існує варіантів вибору студентом іноземної мови та спортивної секції?
У першому ряду кінотеатру встановлено
Спростіть вираз ![]()
Спростіть вираз 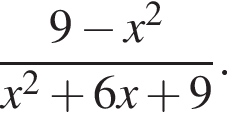
Арифметичну прогресію (an) задано формулою 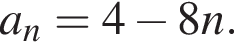 Знайдіть різницю ціеї прогресії.
Знайдіть різницю ціеї прогресії.
Якому з наведених проміжків належить корінь рівняння 
Спростіть вираз 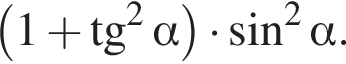
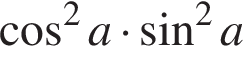
Розв'яжіть рівняння 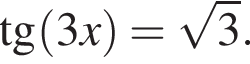
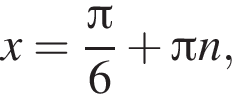
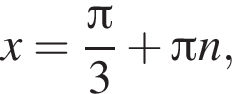
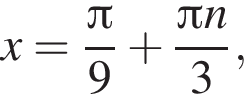
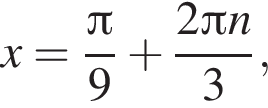
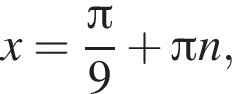
Укажіть найменший додатний корінь рівняння 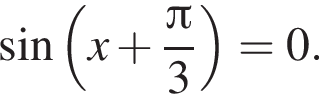
Відомо, що 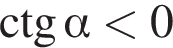 i
i 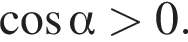 Якого значення може набувати
Якого значення може набувати ![]()
Якщо 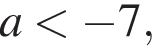 то
то 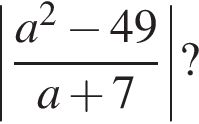
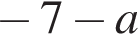
Розв'яжіть нерівність 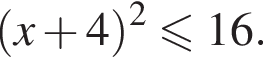
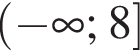
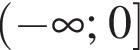
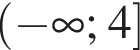
Перетворіть вираз 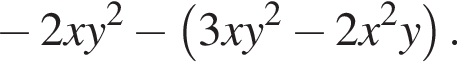
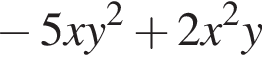
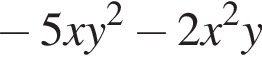
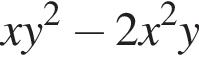
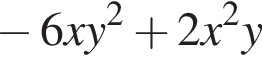
Блок соціальної реклами складається з 4 рекламних роликів: про шкідливість паління, про охорону навколишнього середовища, про дотримання правил дорожнього руху та про велосипедне місто. Ролик про шкідпивість паління заплановано показати двічі — першим і останнім, а інші три ролики — по одному разу. Скільки всього існує варіантів формування цього блоку соціальноі реклами за вказаним порядком рекламних роликів?
Розв'яжіть рівняння 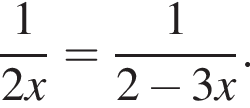
Розв'яжіть систему
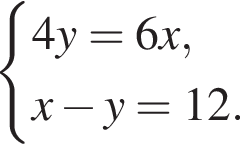
Якщо (x0; y0) — розв'язок цієї системи, то x0?
Обчисливши 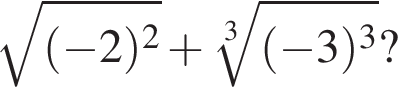
Спростіть вираз 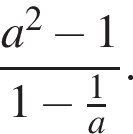
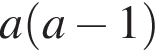
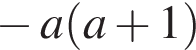
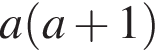
y геометричній прогресії (bn): 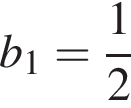 i
i 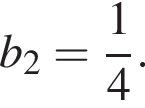 Визначте b4.
Визначте b4.
Якому 3 наведених проміжків належить корінь рівняння 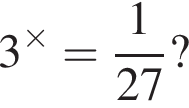
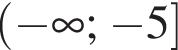

Спростіть вираз 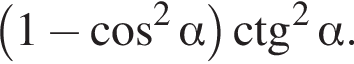
Розв'яжіть нерівність 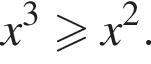


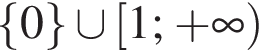
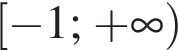
До кожного початку речення (1−4), де ![]()
![]() доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Якщо 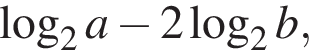 то
то
2. Якщо  то
то
3. Якщо  то
то
4. Якщо 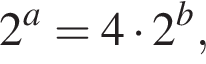 то
то
А 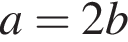
Б 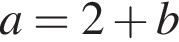
В 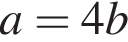
Г ![]()
Д 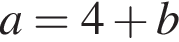
Укажіть запис числа 0,351 у стандартному вигляді.
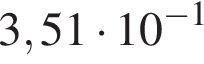
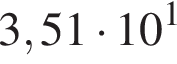
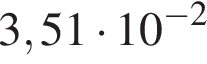
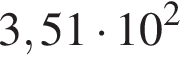
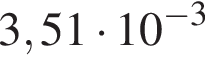
Розв'яжіть рівняння 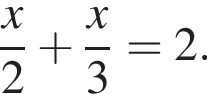
Яка з наведених послідовностей є геометричною прогресією, знаменник якої 
Якщо число b становить 47% від додатного числа а, то b?
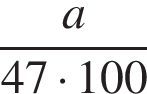
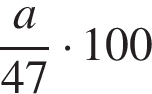
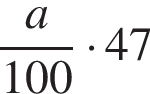
Укажіть проміжок, якому належить корінь рівняння 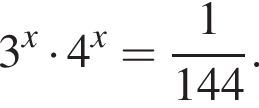
Укажіть правильну нерівність, якщо  i
i 
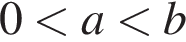
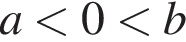
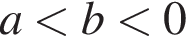
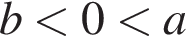
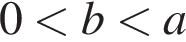
Знайдіть усі значення x, при яких значення виразу ![]() належить проміжку (−3; 6).
належить проміжку (−3; 6).
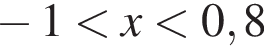
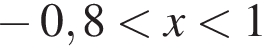
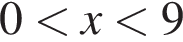
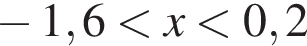
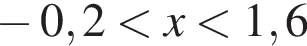
Обчисливши 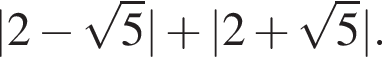
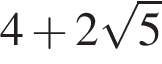
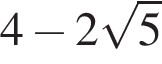
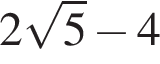
Розв'яжіть нерівність