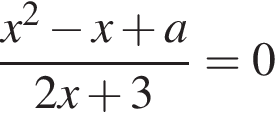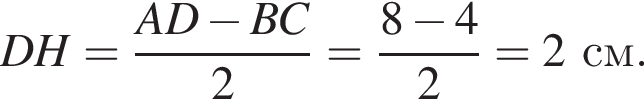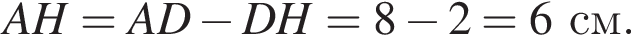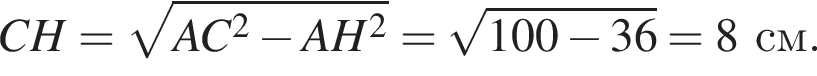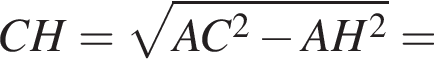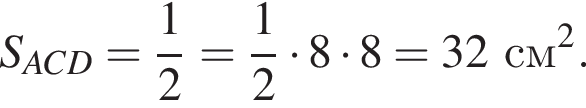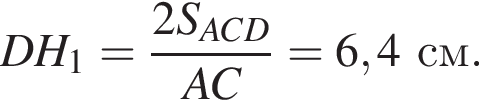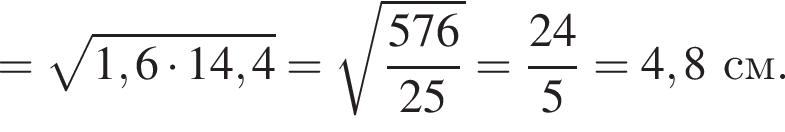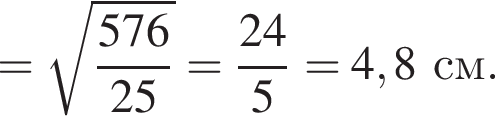Яку 3 наведених цифр потрібно поставити замість зірочки в записі числа ![]() щоб отримане число ділилося націло на 3?
щоб отримане число ділилося націло на 3?
ЗНО 2011 року з математики — пробний тест
Прямі a, b, c попарно перетинаються в точках A, B, C (див. рисунок). За даними, вказаними на рисунку, знаийдіть градусну міру кута ABC.
Обчисліть 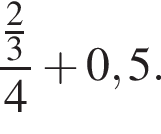
Укажіть хибне твердження.
A) Якщо в чотирикутнику кожна сторона дорівнює протилежній стороні, то такий чотирикутник — паралелограм.
Б) Якщцо всі кути чотирикутника рівні, то такий чотирикутник — прямокутник.
B) Діагоналі прямокутника рівні.
Г) Діагоналі прямокутника є бісектрисами його кутів.
Д) Діагоналі ромба взаємно перпендикулярні.
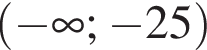
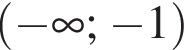
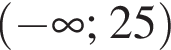
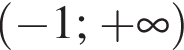
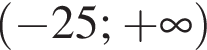
Розв'яжіть нерівність 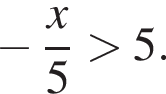
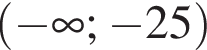
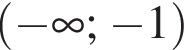
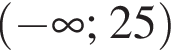
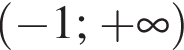
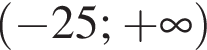
На рисунку зображено вектори
![]() і
і ![]() Який із наведених векторів дорівнює вектору
Який із наведених векторів дорівнює вектору ![]()
Яке з наведених чисеп е ірраціональним числом?
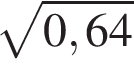
На рисунку зображено три фігури 3 номерами 1, 2, 3. Серед цих фігур укажіть розгортки куба.
Обчисліть 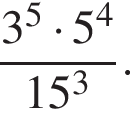
Серед наведених функцій укажіть функцію, область визначення якої збігається з її областю значень.
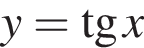


Чотирикутник ABCD описаний навколо кола. Маючи  см,
см, см,
см,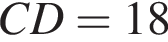 см.
см.
Укажіть рівняння кола з центром у початку координат, якщо воно проходить через точку (3; −4).
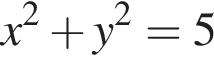
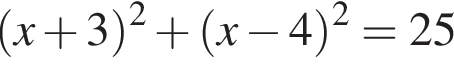
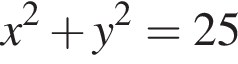
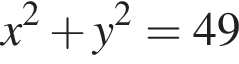

Знайдіть найменший додатний період функції 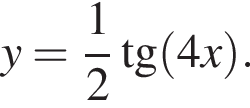
Укажіть суму коренів рівняння 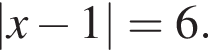
Якщо 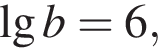 то
то 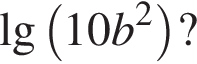
Укажіть рисунок, на якому зображено ескіз графіка функції ![]() при
при ![]()
Якому з наведених проміжків належить корінь рівняння 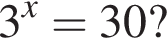
Знайдіть точку, симетричну точці А (2; −3; 7) відносно координатної площини уz.
В арифметичній прогресії (an) 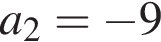 та
та 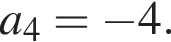 Визначте різницю цієї прогресії.
Визначте різницю цієї прогресії.
Периметр осьового перерізу циліндра дорівнюе 32 см. Знайдіть площу бічної поверхні циліндра, якщо його висота дорівнюе 10 см.
Знайдіть похідну фуннції 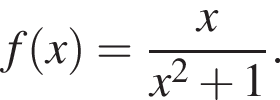
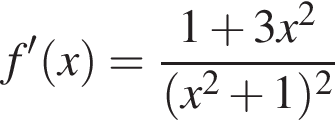
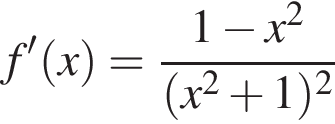
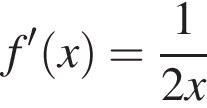
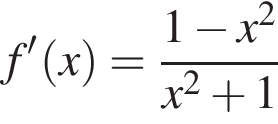
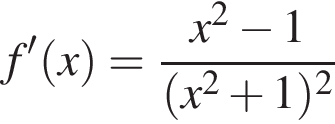
Висота конуса вдвічі менша за діаметр його основи. Знайдіть градусну міру кута між твірною конуса та площиною його основи.
Обчисліть 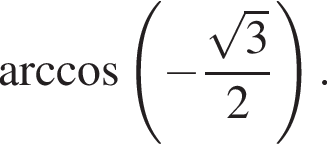
Господарю потрібно зорати город, що має форму прямокутної трапеції. Розміри городу вказано на рисунку. Оранка трактором ділянки площею 100 м2 коштує 8 грн. Скільки грошей (у грн) повинен заплатити господар трактористу за оранку всього городу?
На рисунку зображено графіки функцій
 i
i 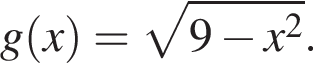 Розв'яжіть нерівність
Розв'яжіть нерівність 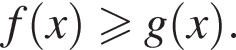

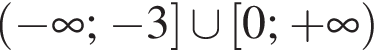

Установіть відповідність між функціями (1−4) та іхніми графіками (А−Д).
1. 
2. 
3. 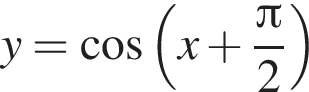
4. 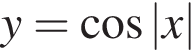
Установіть відповідність між числовими виразами (1−4) та їхніми значеннями (А−Д).
1. 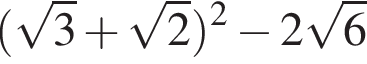
2. 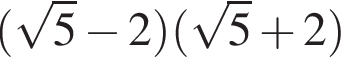
3. 
4. 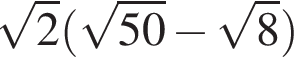
А 15
Б 6
В 5
Г 3
Д 1
На рисунку зображено рівнобедрену трапецію ABCD, у якій
 см,
см, см,
см,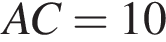 см.
см.
1. проекція видрізка BC на пряму AD
2. проекція видрізка CD на пряму AD
3. проекція видрізка AC на пряму AD
4. проекція видрізка AD на пряму АС
А 2 см
Б 4 см
В 4,8 см
Г 5,6 см
Д 6 см
Знайдіть найбільше значення функції 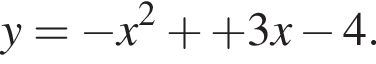 Якщо функція не має найбільшого значення, то у відповідь запишіть число 100.
Якщо функція не має найбільшого значення, то у відповідь запишіть число 100.
Скільки літрів
Заступник директора школи складає розклад уроків для
Знайдіть значення виразу 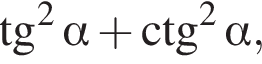 якщо
якщо 
Розв'яжіть нерівність
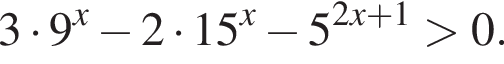
Якщо нерівність має цілі розв'язки, то вкажіть найбільшиŭ 3 них. Якщо нерівність має розв'язки, але вказати найбільший цілий розв'язок неможливо, то у відповідь запишіть число 50. Якщо нерівність не має розв'язків, то у відповідь запишіть число 100.
В основі піраміди лежить прямокутний трикутник із кутом 15°. Усі бічні ребра піраміди нахилені до площини основи під кутом 60°. Радіус кулі, описаноі навколо піраміди, дорівнюе 6 см. Обчисліть об'єм піраміди (у см3).
Укажіть найменше значення a, при якому рівняння